【题解】三角形 [P1222] / 三角形覆盖问题 [HNOI2012] [P3219]

传送门：

【题目描述】

给出 \(n\) 个等腰直角三角的顶点和直角边长，求覆盖总面积。

【输入】

第一行一个整数 \(n\)，表示三角形个数，接下来 \(n\) 行每行三个整数 \(x,y,m\)，分别表示顶点坐标、直角边长（两直角边分别平行于 \(x,y\) 轴且顶点在左下角）。

【输出】

答案保留一位小数。

【样例】

样例输入：

5

-5 -3 6

-1 -2 3

0 0 2

-2 2 1

-4 -1 2

样例输出：

24.5

【数据范围】

\(100 \%:\) \(n \leqslant 2000,\) \(-10^7 \leqslant x,y \leqslant 10^7,\) \(m \leqslant 1000\)【三角形】

\(100 \%:\) \(n \leqslant 10000,\) \(0 \leqslant x,y,m \leqslant 10^6\)【三角形覆盖问题】

【分析】

【计算几何全家桶】

求三角形面积并的板题。

自适应辛普森法乱搞（什么？你说三角形覆盖问题用辛普森过不了？啪）。

代码大致和圆的面积并相同，只需要改几个关键点即可：

\(F\) 函数中求交线（相较于圆变简单了）：

#define LD double

#define Re register int

#define Rd register LD

Re t=0;

for(Re i=1;i<=n;++i)

    if(dcmp(Y-C[i].D)>=0&&dcmp(Y-C[i].U)<0){//如果直线Y与三角形相交

        Rd tmp=C[i].U-Y;//交线长度

        if(dcmp(tmp)>0)Seg[++t]=Segment(C[i].x,C[i].x+tmp);//储存交线

    }

判断小三角形是否被大三角形所包含：

inline int TIT(Triangle A,Triangle B){//判断三角形A是否在三角形B以内

    return A.L>=B.L&&A.R<=B.R&&A.D>=B.D&&A.U<=B.U&&dcmp(A.R-(B.x+B.U-A.y))<=0;

}

完了？

...

\(\text{WA}\) 了！

为什么？

在用辛普森求平面图形面积时，如果对象是圆，那么一定不可能一次性满足精度要求（误差极大），但如果是三角形的话很可能一次计算就结束了递归。

看下图：

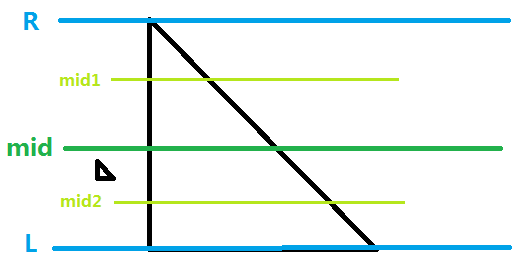
对于第一次递归求解 \((l,r)\)，用公式计算 \(now=Simpson(l,r),FL=Simpson(l,mid),FR=Simpson(mid,r)\) 时使用了上图中的 \(5\) 条横线，发现它们都没有经过左边的小三角形，而此时 \(now,FL,FR\) 都是算的大三角形的准确面积，所以递归会直接终止，最终只返回了大三角形的面积，小三角形被忽略。

为什么算圆面积并时没有出现这种问题呢？前面说了计算对象为圆时不可能一次性满足精度要求，也就是说必定会递归扫描到各个位置，不会存在漏掉某一小块的情况。

解决方案（该思路来自 \(\text{Edgration}\) 巨佬）：

记录所有的 \(y,y+m\) 并排序去重，对于所有相邻两端点所围住的范围单独处理。如下图，分别递归计算 \((Y_1,Y_2),(Y_2,Y_3),(Y_3,Y_4)\) 三块并求和。

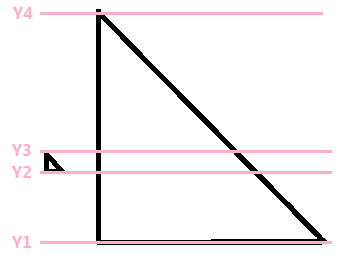
精度！精度！！！

三角形开 \(1e\!-\!9\)，三角形覆盖问题开 \(1e\!-\!10\) 。

调参调出了写模拟退火的感觉

【Code】

#pragma GCC optimize(3,"Ofast","inline")

#include<algorithm>

#include<cstdio>

#include<cmath>

#include<map>

#define LD double

#define LL long long

#define Re register int

#define Rd register LD

#define Vector Point

using namespace std;

const int N=2003;

const LD eps=1e-9;

int n,m;map<LD,LD>vis;

inline int dcmp(Rd a){return a<-eps?-1:(a>eps?1:0);}

struct Point{

    LD x,y;Point(LD X=0,LD Y=0){x=X,y=Y;}

    inline void in(){scanf("%lf%lf",&x,&y);}

};

struct Segment{

    LD L,R;Segment(LD l=0,LD r=0){L=l,R=r;}

    inline bool operator<(Segment O)const{return L!=O.L?L<O.L:R<O.R;}

}Seg[N];

struct Triangle{

	LD x,y,m,L,R,D,U;

	inline void in(){scanf("%lf%lf%lf",&x,&y,&m),L=x,R=x+m,D=y,U=y+m;}

}C[N],C_[N];

inline bool cmp(Triangle A,Triangle B){return A.m<B.m;}//按直角边长排序

inline LD F(Rd Y){

    if(vis[Y])return vis[Y];

    Re t=0;Rd ans=0;

    for(Re i=1;i<=n;++i)

        if(dcmp(Y-C[i].D)>=0&&dcmp(Y-C[i].U)<0){//如果直线Y与三角形相交

            Rd tmp=C[i].U-Y;//交线长度

            if(dcmp(tmp)>0)Seg[++t]=Segment(C[i].x,C[i].x+tmp);//储存交线

        }

    if(!t)return 0.0;

    sort(Seg+1,Seg+t+1);

    for(Re i=1,j;i<=t;i=j+1){

        Rd L=Seg[i].L,R=Seg[i].R;j=i;

        while(j<t&&Seg[j+1].L<=R)++j,R=max(R,Seg[j].R);

        ans+=R-L;

    }

    return vis[Y]=ans;

}

inline LD Simpson(Rd L,Rd R){return (R-L)*(F(L)+4.0*F((L+R)*0.5)+F(R))/6.0;}

inline LD sakura(Rd L,Rd R,Rd now){

    Rd mid=(L+R)*0.5,FL=Simpson(L,mid),FR=Simpson(mid,R);

    if(!dcmp(now-FL-FR))return now;

    return sakura(L,mid,FL)+sakura(mid,R,FR);

}

inline int TIT(Triangle A,Triangle B){//判断三角形A是否在三角形B以内

    return A.L>=B.L&&A.R<=B.R&&A.D>=B.D&&A.U<=B.U&&dcmp(A.R-(B.x+B.U-A.y))<=0;

}

LD ans,YY[N<<1];

int main(){

//  freopen("456.txt","r",stdin);

    scanf("%d",&m);Re t=0;

    for(Re i=1;i<=m;++i)C_[i].in();

    sort(C_+1,C_+m+1,cmp),C[++n]=C_[m];//按半径大小排序

    for(Re i=m-1;i>=1;--i){

        Re flag=1;

        for(Re j=1;j<=n&&flag;++j)if(TIT(C_[i],C[j]))flag=0;

        if(flag)C[++n]=C_[i];

    }

    for(Re i=1;i<=n;++i)YY[++t]=C[i].D,YY[++t]=C[i].U;

    sort(YY+1,YY+t+1);

    for(Re i=2;i<=t;++i)//若干个小块分别处理

        if(dcmp(YY[i]-YY[i-1])>0){

            Rd D=YY[i-1],U=YY[i]-2*eps;//这里必须要偏移边界，否则会死得非常难看

            ans+=sakura(D,U,Simpson(D,U));

        }

    printf("%.1lf",ans);

}