《神经网络的梯度推导与代码验证》之FNN（DNN）的前向传播和反向推导

在《神经网络的梯度推导与代码验证》之数学基础篇：矩阵微分与求导中，我们总结了一些用于推导神经网络反向梯度求导的重要的数学技巧。此外，通过一个简单的demo，我们初步了解了使用矩阵求导来批量求神经网络参数的做法。在篇章，我们将专门针对DNN/FNN这种网络结构进行前向传播介绍和反向梯度推导。

注意：本系列的关注点主要在反向梯度推导以及代码上的验证，涉及到的前向传播相对而言不会做太详细的介绍。

目录

• 2.1 FNN（DNN）的前向传播
• 2.2 FNN（DNN）的反向传播
• 2.3 总结
• 参考资料

---

2.1 FNN（DNN）的前向传播

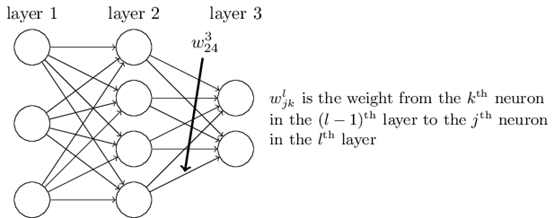
下面是两张DNN的示意图：

我们用$w_{24}^{3}$来表示第2层的第4个神经元与第三层第2个神经元之间的参数。

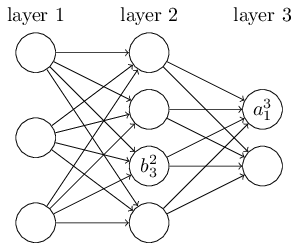
我们用$b_{3}^{2}$表示第2层的第3个神经元的偏置。用$a_{1}^{3}$表示第3层的第1个神经元的输出（注意是经过激活函数后的）。

上图的从第一层到第二层的参数计算公式如下：

$a_{1}^{2} = \sigma\left( {w_{11}^{2}x_{1} + w_{12}^{2}x_{2} + w_{13}^{2}x_{3} + b_{1}^{2}} \right)$

$a_{2}^{2} = \sigma\left( {w_{21}^{2}x_{1} + w_{22}^{2}x_{2} + w_{23}^{2}x_{3} + b_{2}^{2}} \right)$

$a_{3}^{2} = \sigma\left( {w_{31}^{2}x_{1} + w_{32}^{2}x_{2} + w_{33}^{2}x_{3} + b_{3}^{2}} \right)$

$a_{4}^{2} = \sigma\left( {w_{41}^{2}x_{1} + w_{42}^{2}x_{2} + w_{43}^{2}x_{3} + b_{4}^{2}} \right)$

其中$\sigma\left( ~ \right)$表示激活函数。

将上图写成矩阵的编排方式就是下面这样：

$\left\lbrack \begin{array}{l} \begin{array}{l} a_{1}^{2} \\ a_{2}^{2} \\ \end{array} \\ a_{3}^{2} \\ a_{4}^{2} \\ \end{array} \right\rbrack = \sigma\left( {\left\lbrack \begin{array}{lll} \begin{array}{l} w_{11}^{2} \\ w_{21}^{2} \\ \end{array} & \begin{array}{l} w_{12}^{2} \\ w_{22}^{2} \\ \end{array} & \begin{array}{l} w_{13}^{2} \\ w_{23}^{2} \\ \end{array} \\ w_{31}^{2} & w_{32}^{2} & w_{33}^{2} \\ w_{41}^{2} & w_{42}^{2} & w_{43}^{2} \\ \end{array} \right\rbrack\left\lbrack \begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \\ \end{array} \right\rbrack + \left\lbrack \begin{array}{l} \begin{array}{l} b_{1}^{2} \\ b_{2}^{2} \\ \end{array} \\ b_{3}^{2} \\ b_{4}^{2} \\ \end{array} \right\rbrack} \right)$

即

$\boldsymbol{a}^{2} = \sigma\left( {\boldsymbol{W}^{2}\boldsymbol{x} + \boldsymbol{b}^{2}} \right)$

同理得到第二层到第三层的计算公式：

$\boldsymbol{a}^{3} = \sigma\left( {\boldsymbol{W}^{3}\boldsymbol{a}^{2} + \boldsymbol{b}^{3}} \right)$

于是总结下来，DNN的层间关系如下：

$\boldsymbol{a}^{\boldsymbol{l}} = \sigma\left( {\boldsymbol{W}^{l}\boldsymbol{a}^{l - 1} + \boldsymbol{b}^{l}} \right)$

所以DNN的前向传播逻辑如下：

输入：总层数L，所有隐藏层和输出层对应的参数矩阵$\boldsymbol{W}$，偏置向量$\boldsymbol{b}$和输入向量$\boldsymbol{x}$

输出：$\boldsymbol{a}^{L}$

1) 初始化$\boldsymbol{a}^{1} = \boldsymbol{x}$

2) for $l = 2$ to L，计算：$\boldsymbol{a}^{l} = \sigma\left( {\boldsymbol{W}^{l}\boldsymbol{a}^{l - 1} + \boldsymbol{b}^{l}} \right)$

最后的结果即为输出$\boldsymbol{a}^{L}$

---

2.2 FNN（DNN）的反向梯度求导

在进行DNN反向传播算法前，我们需要选择一个损失函数，来度量训练样本计算出的输出和真实的训练样本输出之间的损失。这里用mse作为损失函数，则每一条样本的loss计算公式如下：

$l = \frac{1}{2}\left\| {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right\|_{2}^{2} = \frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)$

其中，$\boldsymbol{y}$就是样本标签$\boldsymbol{y}\_\boldsymbol{t}\boldsymbol{u}\boldsymbol{r}\boldsymbol{e}$，而$\boldsymbol{a}^{\boldsymbol{L}}$就是预测值$\boldsymbol{y}\_\boldsymbol{p}\boldsymbol{r}\boldsymbol{e}\boldsymbol{d}\boldsymbol{i}\boldsymbol{c}\boldsymbol{t}$。

预测值$\boldsymbol{a}^{\boldsymbol{L}}$和输入$\boldsymbol{x}$满足$\boldsymbol{a}^{\boldsymbol{L}} = \boldsymbol{D}\boldsymbol{N}\boldsymbol{N}\left( {\boldsymbol{x};\boldsymbol{W},\boldsymbol{b}} \right)$，这就是2.1中提到的DNN的前向传播过程，这么看来，所谓前向传播，不过是一个复杂的函数罢了。

于是写得再全一点，某条样本$\boldsymbol{a}^{\boldsymbol{L}} = \boldsymbol{D}\boldsymbol{N}\boldsymbol{N}\left( {\boldsymbol{x};\boldsymbol{W},\boldsymbol{b}} \right)$根据mse计算出来的loss就是下面这样：

$l\left( {\boldsymbol{x},\boldsymbol{y},\boldsymbol{W},\boldsymbol{b}} \right) = \frac{1}{2}\left\| {\boldsymbol{D}\boldsymbol{N}\boldsymbol{N}\left\| {\boldsymbol{x};\boldsymbol{W},\boldsymbol{b}} \right\| - \boldsymbol{y}} \right\|_{2}^{2} = \frac{1}{2}\left( {\boldsymbol{D}\boldsymbol{N}\boldsymbol{N}\left( {\boldsymbol{x};\boldsymbol{W},\boldsymbol{b}} \right) - \boldsymbol{y}} \right)^{T}\left( {\boldsymbol{D}\boldsymbol{N}\boldsymbol{N}\left( {\boldsymbol{x};\boldsymbol{W},\boldsymbol{b}} \right) - \boldsymbol{y}} \right)$

铺垫了这么多接下来正式开始求梯度。

我们先求$\frac{\partial l}{\partial\boldsymbol{a}^{\boldsymbol{L}}}$，

$dl = \frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T}d\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right) + \frac{1}{2}d\left( \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T} \right)\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right) = \frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T}d\boldsymbol{a}^{\boldsymbol{L}} + \frac{1}{2}d\left( \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T} \right)\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)$

对$\frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)d\left( \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T} \right)$使用迹技巧，有：

$\frac{1}{2}d\left( \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T} \right)\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right) = \frac{1}{2}tr\left( {d\left( \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T} \right)\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)} \right) = \frac{1}{2}tr\left( {\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{\boldsymbol{T}}d\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)} \right) = \frac{1}{2}tr\left( {\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{\boldsymbol{T}}d\boldsymbol{a}^{\boldsymbol{L}}} \right) = \frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{\boldsymbol{T}}d\boldsymbol{a}^{\boldsymbol{L}}$

所以有：

$dl = \frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T}d\boldsymbol{a}^{\boldsymbol{L}} + \frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{\boldsymbol{T}}d\boldsymbol{a}^{\boldsymbol{L}} = \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{\boldsymbol{T}}d\boldsymbol{a}^{\boldsymbol{L}}$

$\frac{\partial l}{\partial\boldsymbol{a}^{\boldsymbol{L}}} = \boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}$

我们令$\boldsymbol{z}^{L} = \boldsymbol{W}^{\boldsymbol{L}}\boldsymbol{a}^{\boldsymbol{L} - 1} + \boldsymbol{b}^{\boldsymbol{L}}$

可求得$\frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{L}}} = \left( \frac{\partial\boldsymbol{a}^{\boldsymbol{L}}}{\partial\boldsymbol{a}^{\boldsymbol{L}}} \right)^{T}\frac{\partial l}{\partial\boldsymbol{a}^{\boldsymbol{L}}}$

因为$d\boldsymbol{a}^{\boldsymbol{L}} = d\sigma\left( \boldsymbol{z}^{L} \right) = \sigma^{'}\left( \boldsymbol{z}^{L} \right) \odot d\boldsymbol{z}^{L} = diag\left( {\sigma^{'}\left( \boldsymbol{z}^{L} \right)} \right)d\boldsymbol{z}^{L}$

所以$\frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{L}}} = diag\left( {\sigma^{'}\left( \boldsymbol{z}^{L} \right)} \right)\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right) = \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right) \odot \sigma^{'}\left( \boldsymbol{z}^{L} \right)$

有了$\frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{L}}}$，那么求L层的$\boldsymbol{W}^{\boldsymbol{L}}$和$\boldsymbol{b}^{\boldsymbol{L}}$的梯度就非常容易了，根据标量对线性变换的求导结论，直接得到：

$\frac{\partial l}{\partial\boldsymbol{W}^{\boldsymbol{L}}} = \frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{L}}}\left( \boldsymbol{a}^{\boldsymbol{L} - 1} \right)^{T}$

$\frac{\partial l}{\partial\boldsymbol{b}^{\boldsymbol{L}}} = \frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{L}}}$

这样第L层的所有参数的梯度就得到了。

为了方便起见，今后用$\delta^{l}$表示$\frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{l}}}$。

有上面求L层参数的梯度的思路，可以发现，如果我们想求出第$l$层的参数的梯度，我们可以先求出$\delta^{l}$然后直接套用标量对线性变换的求导结论就可以快速求得结果了。因此，这里我们用数学归纳法，第L层的$\delta^{L}$我们已经求出来了，假设第$l+1$层的$\delta^{l + 1}$已求出来，那我们如何求$\delta^{l}$呢？

根据链式法则，有$\frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{l}}} = \left( \frac{\partial\boldsymbol{z}^{\boldsymbol{l} + 1}}{\partial\boldsymbol{z}^{\boldsymbol{l}}} \right)^{T}\frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{l} + 1}}$

现在问题转到求$\frac{\partial\boldsymbol{z}^{\boldsymbol{l} + 1}}{\partial\boldsymbol{z}^{\boldsymbol{l}}}$上。

我们注意到有$\boldsymbol{z}^{l + 1} = \boldsymbol{W}^{l + 1}\sigma\left( \boldsymbol{z}^{\boldsymbol{l}} \right) + \boldsymbol{b}^{l + 1}$成立，

所以$d\boldsymbol{z}^{l + 1} = \boldsymbol{W}^{l + 1}d\sigma\left( \boldsymbol{z}^{\boldsymbol{l}} \right) = \boldsymbol{W}^{l + 1}\left( {\sigma^{'}\left( \boldsymbol{z}^{l} \right) \odot d\boldsymbol{z}^{l}} \right) = \boldsymbol{W}^{l + 1}diag\left( {\sigma^{'}\left( \boldsymbol{z}^{\boldsymbol{l}} \right)} \right)d\boldsymbol{z}^{\boldsymbol{l}}$

所以$\frac{\partial\boldsymbol{z}^{l + 1}}{\partial\boldsymbol{z}^{l}} = \boldsymbol{W}^{l + 1}diag\left( {\sigma^{'}\left( \boldsymbol{z}^{\boldsymbol{l}} \right)} \right)$

于是通过$\delta^{l + 1}$，我们可以求得：

$\delta^{l} = diag\left( {\sigma^{'}\left( \boldsymbol{z}^{\boldsymbol{l}} \right)} \right)\left( \boldsymbol{W}^{l + 1} \right)^{T}\delta^{l + 1} = \left( \boldsymbol{W}^{l + 1} \right)^{T}\delta^{l + 1} \odot \sigma^{'}\left( \boldsymbol{z}^{\boldsymbol{l}} \right)$

同理，根据$\delta^{l + 1}$可以秒求出$\boldsymbol{W}^{l} = \delta^{l}\left( \boldsymbol{a}^{\boldsymbol{l} - 1} \right)^{T}$，$\boldsymbol{b}^{\boldsymbol{l}} = \delta^{l}$

---

2.3 总结

在求神经网络某一层的参数的梯度时，先求出$\delta^{l}$是一种比较合理的策略，因为借助标量对线性变换的求导结论可以快速通过$\delta^{l}$求得参数的梯度；通过推导出$\delta^{l}$与$\delta^{l+1}$的关系，可以将这种求参数梯度的模式推广到其他层上。

同时我们也可以发现，对参数梯度造成影响的因素主要有以下几个：

• 损失函数的选取，它决定了最初的$\frac{\partial l}{\partial\boldsymbol{a}^{\boldsymbol{L}}}$
• 激活函数的选取，它决定了层间$\delta^{l} = \boldsymbol{W}^{\boldsymbol{l} + 1}diag\left( {\sigma^{'}\left( \boldsymbol{z}^{\boldsymbol{l}} \right)} \right)\delta^{l + 1}$的递推计算
• 神经网络的参数，例如每一层的神经元个数影响了$\boldsymbol{W}$的尺寸；而整体深度则影响了神经网络隐藏层（尤其是靠前的隐藏层）的梯度稳定性（靠前的隐藏层可能会发生梯度消失或梯度爆炸）。
• 神经网络的结构，因为显然它会直接影响反向梯度的推导方式（在LSTM的反向梯度推导中大家会有更深的体会）。

---

参考资料

• https://www.cnblogs.com/pinard/p/6422831.html
• https://www.cnblogs.com/pinard/p/6422831.html

（欢迎转载，转载请注明出处。欢迎留言或沟通交流： lxwalyw@gmail.com）