3. Distributional Reinforcement Learning with Quantile Regression

C51算法理论上用Wasserstein度量衡量两个累积分布函数间的距离证明了价值分布的可行性，但在实际算法中用KL散度对离散支持的概率进行拟合，不能作用于累积分布函数，不能保证Bellman更新收敛；且C51算法使用价值分布的若干个固定离散支持，通过调整它们的概率来构建价值分布。

而分位数回归(quantile regression)的distributional RL对此进行了改进。首先，使用了C51的“转置”，即固定若干个离散支持的均匀概率，调整离散支持的位置；引入分位数回归的思想，近似地实现了Wasserstein距离作为损失函数。

Quantile Distribution

假设$\mathcal{Z}_Q$是分位数分布空间，可以将它的累积概率函数均匀分为$N$等分，即$\tau_0,\tau_1...,\tau_N(\tau_i=\frac{i}{N},i=0,1,..,N)$。使用模型$\theta:\mathcal{S}\times \mathcal{A}\to \mathbb{R}^N$来预测分位数分布$Z_\theta \in \mathcal{Z}_Q$，即模型$\{\theta_i (s,a)\}$将状态-动作对$(s,a)$映射到均匀概率分布上。$Z_\theta (s,a)$的定义如下

\[Z_\theta (s,a):=\frac{1}{N}\sum_{i=1}^N \delta_{\theta_i(s,a)} \tag{1}
\]

其中，$\delta_z$表示在$z\in\mathbb{R}$处的Dirac函数

与C51算法相比，这种做法的好处：

不再受预设定的支持限制，当回报的变化范围很大时，预测更精确
取消了C51的投影步骤，避免了一些先验知识
使用分位数回归，可以近似最小化Wassertein损失，梯度下降不再有偏

Quantile Approximation

Quantile Projection

使用1-Wassertein距离对随机价值分布$Z\in \mathcal{Z}$到$\mathcal{Z}_Q$的投影进行量化：

\[\mathcal{\Pi}_{W_1}Z:={\arg\min}_{{Z_\theta}\in\mathcal{Z}_Q}W_1(Z,Z_\theta)
\]

假设$Z_\theta$的支持集为$\{\theta_1,...,\theta_N \}$，那么

\[W_1(Z,Z_\theta)=\sum_{i=1}^N \int_{\tau_{i-1}}^{\tau_i} |F_Z^{-1}(w)-\theta_i|dw
\]

其中，$\tau_i,\tau_{i-1}\in[0,1]$论文指出，当$F_Z^{-1}$是逆累积分布函数时，$F_Z^{-1}((\tau_{i-1}+\tau_i)/2)$最小。因此，量化中点为$\mathcal{\hat\tau_i}=\frac{\tau_{i-1}+\tau_i}{2}(1\le i\le N)$，且最小化$W_1$的支持$\theta_i=F_Z^{-1}(\mathcal{\hat\tau_i})$。如下图

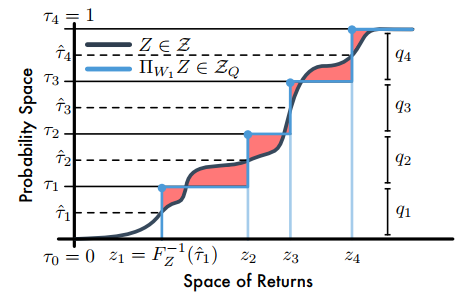
【注】C51是将回报空间(横轴)均分为若干个支持，然后求Bellman算子更新后回报落在每个支持上的概率，而分位数投影是将累积概率(纵轴)分为若干个支持(图中是4个支持)，然后求出对应每个支持的回报值；图中阴影部分的面积和就是1-Wasserstein误差。

Quantile Regression

建立分位数投影后，需要去近似分布的分位数函数，需要引入分位数回归损失。对于分布$Z$和一个给定的分位数$\tau$，分位数函数$F_Z^{-1}(\tau)$的值可以通过最小化分位数回归损失得到

\[\mathcal{L}_{\text{QR}}^\tau(\theta):=\mathbb{E}_{\hat Z\sim Z}[\rho_\tau (\hat Z -\theta)],\quad \text{where} \quad \rho_\tau (u)=u(\tau-\delta_\{u<0\}),\forall u\in\mathbb{R}
\]

最终，整体的损失函数为

\[\sum_{i=1}^N \mathbb{E}_{\hat Z\sim Z}[\rho_{\hat{\tau}_i} (\hat Z -\theta)]
\]

但是，分位数回归损失在0处不平滑。论文进一步提出了quantile Huber loss：

\[\mathcal{L}_{\mathcal{K}}(u)=
\begin{cases}
& \frac{1}{2}u^2,\quad\quad\quad\quad \text{if} |u|\le \mathcal{K} \\
& \mathcal{K}(|u|-\frac{1}{2}\mathcal{K}),\,\, \text{otherwise}
\end{cases}
\]

\[\rho_{\tau}^{\mathcal{K}}(u)=|\tau-\delta_{\{u<0\}}|\mathcal{L}_{\mathcal{K}}(u)
\]

Implement

QR TD-Learning

QRTD算法(quantile regression temporal difference learning algorithm)的更新

\[\theta_i(s)\leftarrow \theta_i(s)+\alpha (\hat{\mathcal{\tau}}_i-\delta_{\{r+\gamma z^\prime < \theta_i (s) \}})
\]

$a\sim\pi (\cdot|s),r\sim R(s,a),s^\prime\sim P(\cdot|s,a),z^\prime\sim Z_\theta(s^\prime)$

其中，$Z_\theta$是由公式(1)给出的分位数分布，$\theta_i (s)$是状态$s$下$F_{Z^\pi (s)}^{-1}(\mathcal{\hat \tau}_i)$的估计值。

QR-DQN

QR-DQN算法伪代码

Append

1. Dirac Delta Function

\[\delta_a (x)=\delta (x-a)=0,(x\neq 0) \quad且\quad \int_{-\infty}^\infty \delta_a (x)d_x=1
\]

References

Will Dabney, Mark Rowland, Marc G. Bellemare, Rémi Munos. Distributional Reinforcement Learning with Quantile Regression. 2017.

Distributional RL