随机森林——Random Forests

[基础算法] Random Forests

2011 年 8 月 9 日

Random Forest(s)，随机森林，又叫Random Trees[2][3]，是一种由多棵决策树组合而成的联合预测模型，天然可以作为快速且有效的多类分类模型。如下图所示，RF中的每一棵决策树由众多split和node组成：split通过输入的test取值指引输出的走向（左或右）；node为叶节点，决定单棵决策树的最终输出，在分类问题中为类属的概率分布或最大概率类属，在回归问题中为函数取值。整个RT的输出由众多决策树共同决定，argmax或者avg。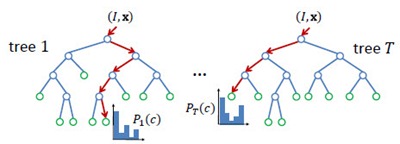

Node Test
node test通常很简单，但很多简单的拧在一起就变得无比强大，联合预测模型就是这样的东西。node test是因应用而异的。比如[1]的应用是基于深度图的人体部位识别，使用的node test是基于像素x的深度比较测试：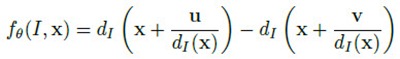


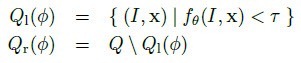
简单的说，就是比较像素x在u和v位移上的像素点的深度差是否大于某一阈值。u和v位移除以x深度值是为了让深度差与x本身的深度无关，与人体离相机的距离无关。这种node test乍一看是没有意义的，事实上也是没多少意义的，单个test的分类结果可能也只是比随机分类好那么一丁点。但就像Haar特征这种极弱的特征一样，起作用的关键在于后续的Boosting或Bagging——有效的联合可以联合的力量。

Training
RF属于Bagging类模型，因此大体训练过程和Bagging类似，关键在于样本的随机选取避免模型的overfitting问题。RF中的每棵决策树是分开训练的，彼此之间并无关联。对于每棵决策树，训练之前形成一个样本子集，在这个子集中有些样本可能出现多次，而另一些可能一次都没出现。接下去，就是循序决策树训练算法的，针对这个样本子集的单棵决策树训练。
单棵决策树的生成大致遵循以下过程：
1）随机生成样本子集；
2）分裂当前节点为左右节点，比较所有可选分裂，选取最优者；
3）重复2）直至达到最大节点深度，或当前节点分类精度达到要求。
这一过程是贪婪的。
当然对于不同的应用场合，训练过程中，会有细节上的差别，比如样本子集的生成过程、以及最优分割的定义。
在[1]中，决策树的真实样本其实是图片中的像素x，变量值则是上文提到的node test。但是，对于一张固定大小的图片而言可取的像素x是可数大量的，可取的位移(u，v)和深度差阈值几乎是不可数无限的。因此，[1]在训练单棵决策树前，要做的样本子集随机其实涉及到像素x集合的随机生成、位移(u，v)和深度差阈值组合的随机生成，最后还有训练深度图集合本身的随机生成。
最优分裂通常定义为使信息增量最大的分类，如[1]中的定义：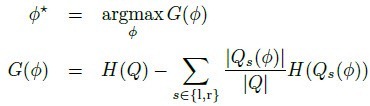

H指熵，通过分裂子集的部位标签分布计算。

---

Reference：
[1] J. Shotton, A. Fitzgibbon, M. Cook, T. Sharp, M. Finocchio, R. Moore, A. Kipman, and A. Blake. Real-Time Human Pose Recognition in Parts from a Single Depth Image. In CVPR 2011.
[2] L. Breiman. Random forests. Mach. Learning, 45(1):5–32, 2001.
[3] T. Hastie, R. Tibshirani, J. H. Friedman. The Elements of Statistical Learning. ISBN-13 978-0387952840, 2003, Springer.
[4] V. Lepetit, P. Lagger, and P. Fua. Randomized trees for real-time keypoint recognition. In Proc. CVPR, pages 2:775–781, 2005

转自http://lincccc.com/?p=47

from: http://blog.csdn.net/yangtrees/article/details/7488937