POJ 1191 棋盘分割（DP）

题目链接

题意 ： 中文题不详述。

思路 ： 黑书上116页讲的很详细。不过你需要在之前预处理一下面积，那样的话之后列式子比较方便一些。

先把均方差那个公式变形，

另X表示x的平均值，两边平方得

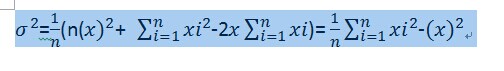平均值是一定的，所以只要让每个矩形的总分的平方和尽量小即可。左上角坐标为（x1,y1）右下角坐标为(x2,y2)的棋盘，设总和为s[][][][]，切割k次以后得到k+1块矩形的总分平方和是d[k][][][][],则可以沿着横线切也可以沿着竖线切，然后选一块接着切，递归下去，状态转移方程

d[k,x1,y2,x2,y2] = min{min{d[k-1,x1,y1,a,y2]+s[a+1,y1,x2,y2],d[k-1,a+1,y1,x2,y2]+s[x1,y1,a,y2]}(x1<=a<x2),min{d[k-1,x1,y2,x2,b]+s[x1,b+1,x2,y2],d[k-1,x1,b+1,x2,y2]+s[x1,y1,x2,b]},(y1<=b<y2)}

 //
 #include <stdio.h>
 #include <iostream>
 #include <cmath>

 using namespace std ;

 double dp[][][][][] ,s[][] ;
 int n ;

 double ss(int x1,int y1,int x2,int y2)
 {
     double sss = s[x2][y2]-s[x1-][y2]-s[x2][y1-]+s[x1-][y1-] ;
     return sss * sss ;
 }

 double DFS(int k,int x1,int y1,int x2,int y2)
 {
     if(k == ) return ss(x1,y1,x2,y2) ;
     if(fabs(dp[k][x1][y1][x2][y2]) > 1e-) return dp[k][x1][y1][x2][y2] ;
     double minn =  <<  ;
     for(int i = x1 ; i < x2 ; i++)
         minn = min(minn,min(DFS(k-,x1,y1,i,y2)+ss(i+,y1,x2,y2),DFS(k-,i+,y1,x2,y2)+ss(x1,y1,i,y2))) ;
     for(int i = y1 ; i < y2 ; i++)
         minn = min(minn,min(DFS(k-,x1,y1,x2,i)+ss(x1,i+,x2,y2),DFS(k-,x1,i+,x2,y2)+ss(x1,y1,x2,i))) ;
     dp[k][x1][y1][x2][y2] = minn ;
     return minn ;
 }
 int main()
 {
     scanf("%d",&n) ;
     int x ;
     //memset(s,0,sizeof(s)) ;
     for(int i =  ; i <=  ; i++)
         for(int j =  ; j <=  ; j++)
         {
             scanf("%d",&x) ;
             s[i][j] = x + s[i-][j]+s[i][j-]-s[i-][j-] ;
         }
         printf("%.3lf\n",sqrt(DFS(n,,,,)/n-(s[][]/n)*(s[][]/n)) );
     return  ;
 }