vijosP1289 老板娘的促销方案

vijosP1289 老板娘的促销方案

链接：https://vijos.org/p/1289

【思路】

组合公式+高精度。

如果n-m<2则无解。

否则对于第一个询问：ans=C(n-m,2)+C(n-m,3)=C(n-m+1,3)。对于第二个询问：

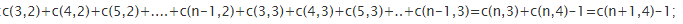
由此可见，对于递推式的化简也是很重要的，可以有效简化求解。

不管有没有陷阱，反正我用高精度=_=。高精度一定要写熟练，如臂指使。

【代码】

 #include<iostream>
 using namespace std;
 struct Bign{
     int len;
     long long N[];
     Bign() {
         for(int i=;i<;i++) N[i]=;
     }
 };
 int n,m;

 void multi(Bign& a,int x)
 {
     for(int j=;j<a.len;j++) a.N[j] *= x;
     int i=;
     while(i<a.len || a.N[i]>) {
         a.N[i+] += a.N[i]/;
         a.N[i] %= ;
         i++;                    //i++
     }
     if(a.N[i]) a.len=i+;
     else a.len=i;
 }

 void div(Bign& a,int x) {
     for(int i=a.len-;i>;i--) {
         a.N[i-] += a.N[i]%x*;
         a.N[i] /= x;
     }
     while(a.N[a.len-]==) a.len--;
     a.N[]/=x;
 }

 int main() {
     Bign C; C.len=; C.N[]=;

     cin>>n>>m;
     if(n-m<) cout<<"NO!\n";
     else
     {
             int k=n-m+;
             for(int i=k-;i<=k;i++) multi(C,i);
             div(C,);
             for(int i=C.len-;i>=;i--) cout<<C.N[i];
             cout<<"\n";
     }
     Bign C2; C2.len=; C2.N[]=;
     for(int i=n-;i<=n+;i++) multi(C2,i);
     div(C2,);

     if(C2.N[]==) {
         C2.N[]--;
         C2.N[]+=;
     }
     C2.N[]-=;
     for(int i=;i<C2.len;i++) if(C2.N[i]<) {
         C2.N[i]+=;
         C2.N[i+]--;
     }
     for(int i=C2.len-;i>=;i--) cout<<C2.N[i];
     return ;
 }