PTA L2-4 关于堆的判断

　　　　先上题面　　

链接 https://pintia.cn/problem-sets/994805046380707840/problems/994805064676261888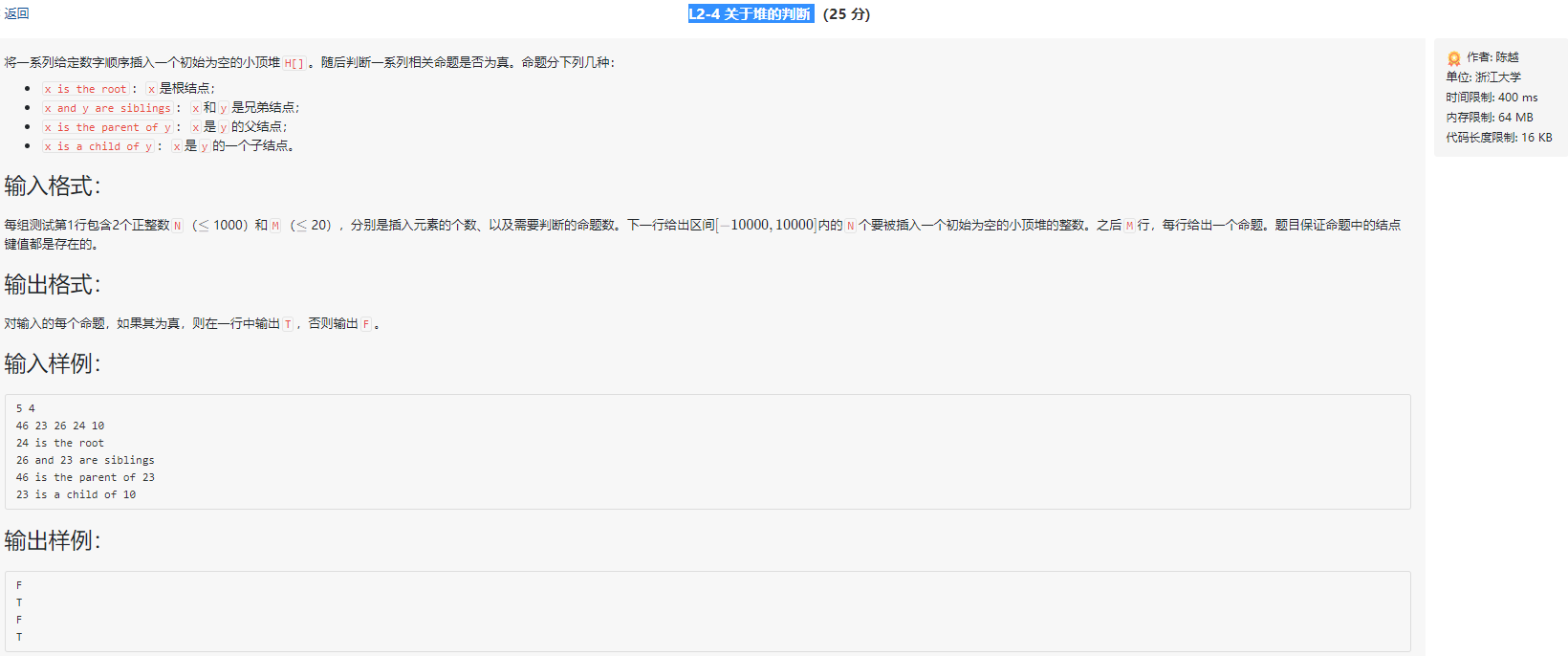

　　首先，题目描述的很清楚，这是一个关于最小堆的问题。题目的意思就是根据插入顺序建一个最小堆，然后对给出的命令进行判断，输出T or F。

　　因为堆其实就是一种特殊的二叉树，它具有两个性质: 1.结构性：用数组表示的完全二叉树。

　　　　　　　　　　　　　　　　　　　　　　　　　　2. 有序性：任一结点的关键字是其子树所有结点的最大值（最大堆）或最小值（最小堆）。

按照上述，我们应该很容易想到用数组存储这个堆，因为这样方便的进行元素的插入以及交换。

接下来就是进行建堆操作

其操作如下：

1.先将要插入的元素放在数组的末尾。

2.进行上浮交换操作，如果它小于它的父节点(在数组中表示为 i/2 )，则就进行交换。

3.不断插入元素，重复执行1，2操作。

完成建堆操作后，因为接下来进行的查询操作给出的是值，而我们则要根据下标来判断他们之间的关系。

所以要建立一个map映射关系，同时，因为查询中有父子结点的关系的判断，因此可以开个数组存储父子节点关系。

最后，就是执行查询操作了，输入的查询语句有一定规律，这个将在下面的代码中展示。

tips：因为输入的值存在负值，所以可以令num[0] = -1001，令num[1] - num[N]存值，这样才能保证建堆正确。

#include <cstdio>
#include <vector>
#include <map>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
int H[],fa[],depth[];
map<int,int>mp;
void dui(int val,int site)
{
    for(;val<H[site/]&&site>;site/=)
    {
        swap(H[site],H[site/]);
    }

    return ;
}
int main()
{
    int n,m;
    scanf("%d %d",&n,&m);
    scanf("%d",&H[]);
    H[] = -;
    for(int i = ;i<=n;i++)
    {
        scanf("%d",&H[i]);
        dui(H[i],i);
    }
    for(int i = ;i<=n;++i)
        mp[H[i]] = i;
    fa[] = ;
    for(int i = ;i<=n;i++)
    {
        fa[i] = H[i/];

    }
    int a,b;
    string s;
    while(m--)
    {
        bool flag;
        scanf("%d",&a);
        cin >> s;
        if(s=="is")
        {
            cin >>s>>s;
            if(s=="root")
            {
                if(H[]==a)
                    flag = true;
                else
                    flag = false;
            }
            else if(s=="child")
            {
                cin >> s;
                scanf("%d",&b);
               // printf("a==%d b==%d\n",a,b);
                if(fa[mp[a]]==b)
                    flag = true;
                else
                    flag = false;
            }
            else
            {
                cin >> s;
                scanf("%d",&b);
                if(fa[mp[b]]==a)
                flag = true;
                else
                    flag  = false;

            }
        }
        else
        {
            scanf("%d",&b);
            cin >>s >>s;
            if(fa[mp[a]]==fa[mp[b]])
                flag = true;
            else
                flag = false;
        }
    if(flag)
        printf("T\n");
    else
        printf("F\n");
    }

   return ;
}

如果有所帮助，不胜荣幸。