JVM虚拟机和垃圾回收算法

• 类加载机制
• 双亲委派模型
• 垃圾回收算法
• CMS G1

类加载机制

双亲委派模型

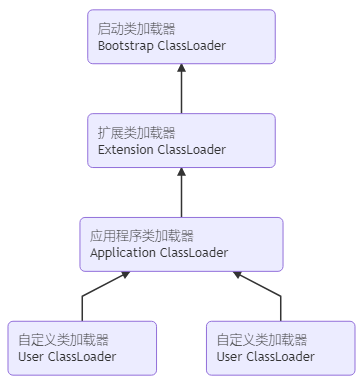
双亲委派模型: 需要加载一个类,先委托父类加载,父类找父类,依次递归加载;加载不到再由自己加载

垃圾回收算法

JVM的内存结构包括五大区域：程序计数器、虚拟机栈、本地方法栈、堆区、方法区.

程序计数器、虚拟机栈、本地方法栈, 随线程来,随线程去,不用关心
堆区 使用引用计数法、可达分析法进行回收
方法区 需要操作回收

a.标记-清除算法(Mark-Sweep)

b.复制算法(Copying)

c.标记-整理算法(Mark-Compact)

• 该类所有的实例都已经被回收，也就是Java堆中不存在该类的任何实例；
• 加载该类的ClassLoader已经被回收；
• 该类对应的java.lang.Class对象没有在任何地方被引用，无法在任何地方通过反射访问该类的方法。

d.分析收集算法

• 新生代Young Generation (Copying 快速腾空内存)[eden区:survivor0: survivor1=8:1:1]
• 老年代 Old Generation(Mark-Compact)
• 持久代Permanent Generation(也称方法区)

CMS G1

CMS（Concurrent Mark Sweep）收集器是基于“标记-清除”算法实现的。整个过程分为6个步骤，包括：

1. 初始标记（CMS initial mark）
2. 并发标记（CMS concurrent mark）
3. 并发预清理（CMS-concurrent-preclean）
4. 重新标记（CMS remark）
5. 并发清除（CMS concurrent sweep）
6. 并发重置（CMS-concurrent-reset）

G1收集器 基于“标记-整理”算法实现的收集器

参考:

• https://blog.csdn.net/xu768840497/article/details/79175335
• https://www.cnblogs.com/aspirant/p/8662690.html
• http://www.zicheng.net/article/55.htm