Kruskal重构树入门

这个知识点好像咕咕咕了好长了。。趁还没退役赶紧补一下吧。。

讲的非常简略，十分抱歉。。

前置知识

Kruskal算法

一定的数据结构基础(如主席树)

Kruskal重构树

直接bb好像不是很好讲，那就从这道题入手吧。

在Bytemountains有$N$座山峰，每座山峰有他的高度$h_i$。

有些山峰之间有双向道路相连，共$M$条路径，每条路径有一个困难值，这个值越大表示越难走.

现在有$Q$组询问，每组询问询问从点$v$开始只经过困难值小于等于$x$的路径所能到达的山峰中第$k$高的山峰，如果无解输出$-1$

首先，这是一张图(你在说大实话么)

对于一个点来说，经过困难值小于等于$x$的路径所能到达的点是一定的。

但是这和生成树有啥关系呢？

显然，若一个点能通过一条路径到达，那么我们走最小生成树上的边也一定能到达该节点。

这样我们把最小生成树建出来，就可以少考虑很多边了。

然而并没有什么卵用。。

现在我们需要做的，是找一种方法，能够维护出一个点能到达的点。

于是Kruskal重构树就诞生了。

它的思想是这样的：

在运行Kruskal算法的过程中，对于两个可以合并的节点$(x, y)$，断开其中的连边，并新建一个节点$T$，把$T$向$(x, y)$连边作为他们的父亲，同时把$(x, y)$之间的边权当做$T$的点权

比如说

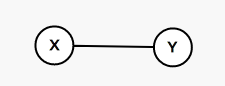
重构之后是这样的：

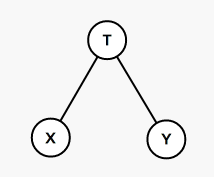
这样我们得到了一个新的树，考虑它有什么性质。

其中最重要的一条就是：一个节点能走到的节点一定在它的子树中

然后这道题就做完了，直接dfs序+主席树即可

当然，除了这一条之外，Kruskal重构树还有很多有意思的性质

1. 是一个二叉树
2. 如果是按最小生成树建立的话是一个大根堆(important!)
3. 任意两个点路径上边权的最大值为它们的LCA的点权

例题

[NOI2018]归程