数位dp相关
经典的数位Dp是要求统计符合限制的数字的个数。
一般的形式是:求区间[n,m]满足限制f(1)、 f(2)、 f(3)等等的数字的数量是多少。 条件 f(i) 一般与数的大小无关,而与数的组成有关。
善用不同进制来处理,一般问题都是10进制和二进制的数位dp。
数位dp的部分一般都是很套路的,但是有些题目在数位dp外面套了一个华丽的外衣,有时我们难以看出来。
直接就上的例题:
HDU3652
统计区间[1,n]中含有'13'且模13为0的数字有多少个。
N<=1e9;
咋做?不急,先从简化版的找规律;
HDU3652简化版
统计区间 [1,n] 中含有 '3' 的数字有多少个。
N=x_1 x_2 x_3 x_4….. x_total 。 x_i为n的从高到低第i位是多少。 Total是总的位数。
如果我们考虑从高到低位不断填数y_1 y_2 …。那么问题其实就是问有多少填数的方案,一要满足上限的限制(对应区间[1,n]),二要满足题目的其他限制。
这样其实就比[1,n]看起来更能dp了
假设到了第k位y_k!=x_k,则k位之后就没有上限的限制了,情况就简化了。
如果前面y中没有出现3:那么假如我们可以求出来, f[k][0]表示k位之后没有上限限制(随意填),但是必须填个3(前面没有出现),有多少种填数的方案。
如果前面y中出现了3:那么假如我们可以求出来, f[k][1]表示k位之后没有上限限制(随意填),没有必须出现3的限制(前面出现过了),有多少种填数的方案。
首先我们可以枚举到哪一位y_k!=x_k,然后再枚举这一位是多少,把对应的F加起来就是答案了,一共需要加 位数*10 次。这运算次数是不大的。
而f数组总大小也很小, 位数*2。

边界 f[total+1][0]=0,f[total+1][1]=1,转移复杂度O(10)
◦总复杂度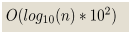
那回归到原题呢?
枚举哪一位不同没什么变化吧,跟原先一样枚举就好了。
就是f数组要变,因为约束条件更多了,所以状态的维数要增加。
设f[k][前面是否已经出现13][上一位是否是1][前面的那些数mod13等于多少],转移的话同样还是枚举这一位是填什么即可。
f[0][1][1/0][0]=1; else =0;such as f[0][0][1/0][1~12]=0;
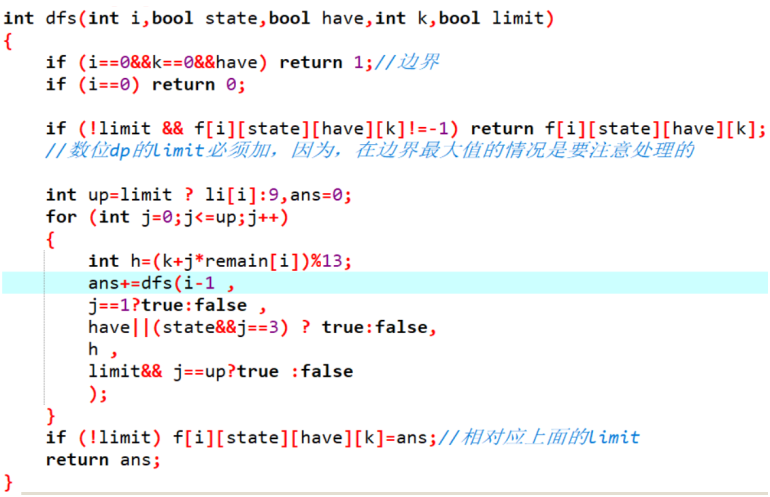
用记忆化搜索实现:
i表示到了第几位。
State:上一位是否为1。
Have:是否已经有13.
K:已经加上的数mod13的值。
注意只有不顶到上界才能记忆化下来答案。
remain[i]=1e(i-1)
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream> using namespace std; int cnt;
int s[];
int t[]={,,,,,,,,,,,};
int f[][][][]; int dfs(int limits,int i,int num,bool have,int ret){
if(i==&&have&&ret==) return ;
if(i<=) return ;
if(!limits&&f[i][num][have][ret]!=-) return f[i][num][have][ret];
int up;
if(limits) up=s[i];
else up=;
int ans=;
for(int j=;j<=up;j++){
int h=(ret+t[i-]*j)%;
ans+=dfs(limits&&j==up?:,i-,j,have||(num==&&j==),h);
}
if(!limits) f[i][num][have][ret]=ans;
return ans;
} int main(){
int n;
while(scanf("%d",&n)==){
memset(s,,sizeof(s));
memset(f,-,sizeof(f));
cnt=;
while(n){
s[++cnt]=n%;
n/=;
}
cout<<dfs(,cnt,,,)<<endl;
}
return ;
}
然后其他例题:1:统计区间 [m,n] 中4和7不能同时出现的数字有多少个?
2:给你一个区间[n,m],要你求区间内不含“62”或“4”的数字的个数?
3: bzoj1026: windy定义了一种windy数。 不含前导零且相邻两个数字
之差至少为2的正整数被称为windy数。 windy想知道,在A和B之间,包
括A和B,总共有多少个windy数?
hdu3079
题中平衡数的定义: 以一个位置作为平衡轴,然后左右其他数字本身大小作为重量,到平衡轴的距离作为权值,实现左右平衡(即杠杆原理平衡)。然后为区间[x,y]内平衡数的个数。 (0 ≤ x ≤ y ≤10^18 )
单纯的,我们可以考虑到,对于任意非0数,如果有中心轴,它的中心轴必定只有一个。
我们以中心轴来进行数位dp即可;
bzoj3209
设 sum(i) 表示 i 的二进制表示中 1 的个数。给出一个正整数 N ,花神要问你派(Sum(i)),也就是 sum(1)—sum(N) 的乘积。答案对一个质数取模。 对于 100% 的数据, N≤10^15
我们可以尝试枚举一个k,然后用数位dp求一共有多少个数有k个1,求出数量后显然ans*=k^数量,快速幂就可以了,但是要注意的一点是爆int;

bzoj4521: [Cqoi2016]手机号码
数字L到R中有多少个数字满足以下两个条件。
1:要出现至少3个相邻的相同数字
2:号码中不能同时出现8和4。
10^10 < = L < = R < 10^11
dfs(i, same, last, appear, occur8, occur4, limit)
Same:上一位和上上一位是否相同
Last:上一位数字 Appear:连续三个相同是否出现过。
Occur4: 4是否出现过?
Occur8: 8是否出现过?
还用记前导0吗?不用
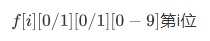
数位dp相关的更多相关文章
- 2019牛客多校第六场H Pair(数位DP 多个数相关)题解
题意: 传送门 给你\(A,B,C\),要求你给出有多少对\((x, y)\)满足\(x\in [1,A],y\in [1,B]\),且满足以下任意一个条件:\(x \& y > C\) ...
- hdoj4734(数位dp优化)
题目链接:https://vjudge.net/problem/HDU-4734 题意:定义一个十进制数AnAn-1...A1的value为An*2n-1+...+A1*20,T组样例(<=1e ...
- Luogu4345 SHOI2015 超能粒子炮·改 Lucas、数位DP
传送门 模数小,还是个质数,Lucas没得跑 考虑Lucas的实质.设\(a = \sum\limits_{i=0}^5 a_i 2333^i\),\(b = \sum\limits_{i=0}^5 ...
- 数位DP详解
算法使用范围 在一个区间里面求有多少个满足题目所给的约束条件的数,约束条件必须与数自身的属性有关 下面用kuangbin数位dp的题来介绍 例题 不要62 题意:在一个区间里面求出有多少个不含4和6 ...
- 51Nod 1009 数字1的个数 | 数位DP
题意: 小于等于n的所有数中1的出现次数 分析: 数位DP 预处理dp[i][j]存 从1~以j开头的i位数中有几个1,那么转移方程为: if(j == 1) dp[i][j] = dp[i-1][9 ...
- BZOJ1799 [Ahoi2009]self 同类分布[数位DP]
求出[a,b]中各位数字之和能整除原数的数的个数. 有困难的一道题.被迫看了题解:枚举每一个各位数字的和($<=162$),设计状态$f[len][sum][rest]$表示dp后面$len$位 ...
- HDU 4722:Good Numbers(数位DP)
类型:数位DP 题意:定义一个Good Number 为 一个数所有位数相加的和%10==0.问[A,B]之间有多少Good Number. 方法: 正常“暴力”的定义状态:(i,d,相关量) 定义d ...
- 数位dp对于状态描述与发现的一些感悟
今天刷的数位dp 第一题看了题解以后知道了数位dp的基本板子,写数位dp的方式(运用记忆化递归的方法)已经基本固定. 那么接下来的难点主要还是对于题目描述的问题,如何抽象成dp中的状态.就今天刷的题来 ...
- 算法-数位dp
算法-数位dp 前置知识: \(\texttt{dp}\) \(\texttt{Dfs}\) 参考文献 https://www.cnblogs.com/y2823774827y/p/10301145. ...
随机推荐
- JVM调优总结(三)——分代垃圾回收详述
为什么要分代 分代的垃圾回收策略,是基于这样一个事实:不同的对象的生命周期是不一样的.因此,不同生命周期的对象可以采取不同的收集方式,以便提高回收效率. 在Java程序运行的过程中,会产生大量的对象, ...
- hbase字典顺序表(即ASCII码表顺序)
- 对js数组去重的研究
1.利用es5 let arr = [1, 2, 3, 4, 5, 6, 7, 1, 2, 3] const unique=arr=>{ return Array.from(new Set(ar ...
- 编译caffe-gpu-cuda及cudnn-tar 下载地址
y下载 https://github.com/BVLC/caffe https://github.com/BVLC/caffe/archive/master.zip gcc caffe安装 有2个问题 ...
- jquery eq()选择器 语法
jquery eq()选择器 语法 作用::eq() 选择器选取带有指定 index 值的元素.index 值从 0 开始,所有第一个元素的 index 值是 0(不是 1).经常与其他元素/选择器一 ...
- JPA学习(六、JPA_JPQL)
框架学习之JPA(六) JPA是Java Persistence API的简称,中文名Java持久层API,是JDK 5.0注解或XML描述对象-关系表的映射关系,并将运行期的实体对象持久化到数据库中 ...
- 数据:ContentResolver类
ContentResolver是通过URI来查询ContentProvider中提供的数据.除了URI以 外,还必须知道需要获取的数据段的名称,以及此数据段的数据类型. 如果你需要获取一个特定的记 ...
- 7.28Assignment
1.考试题(7.27) + 2.插头dp 4道题 0/4 before 18:00 3.cdq分治 2道题理解 0/2 before 21:00 4.点分治 2道题 0/2 before 7:00 ...
- ROI pooling
R-CNN需要大量的候选框,对每个候选框都提取特征,速度很慢,无法做到实时检测,无法做到端到端.ROI pooling层实现training和testing的显著加速,并提高检测accuracy. R ...
- 在最新的 create-react-app 中添加 less 支持
前置知识: 把 webpack 的相关配置暴露出来 运行 git add -A 运行 git commit -m 'project init' 运行 yarn eject 然后选 y 项目中多出来两个 ...
