codeforces_D. Treasure Hunting_[DP+Binary Search]

http://codeforces.com/contest/1201/problem/D

题意：n行m列的矩阵中，有k个targets，从[1, 1]出发，每次只能向上下左右四个方向移动一步，且只有在q个safecolumns上进行向上移动，最少需要多少次移动才能获得所有的targets。(2≤n,m,k,q≤2*10^5,q≤m)。

  

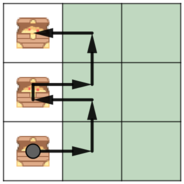
思路：

Make two arrays: left and right. left[i] is the treasure in the leftmost position in row i (0 if there are no treasures in row ii). right[i] is the treasure in the rightmost cell in row ii (0 if there are no treasures in row ii).

We can simply take out rows where there is no treasure (and add 1 to the result if there are treasure above that line, because we have to move up there).

For every row, except the last, we have to leave that row at one of the safe columns. Let's notice that the last treasure we collect in the row will be either left[i] or right[i]. Let's take a look at both possibilities: If we collect the left[i] treasure last, we have to leave the row either going left or going right to the closest safe column, because going further wouldn't worth it (consider moving up earlier and keep doing the same thing at row i+1). The same is true for right[i]. For the first row, we start at the first column, we can calculate the moves required to go up the second row at the for cells. For all the other rows, we have 4 possibilities, and we have to calculate how many moves it takes to reach the row i+1 at the 4 possible columns. For the last row, we don't have to reach a safe column, we just have to collect all the treasures there. We can count the answer for the problem from the calculated results from the previous row. Time complexity: O(16∗n)

1. 对于存在宝藏的行，最后得到的宝藏要么是最左边的要么是最右边的；

2. 假设最后拿到的是最左边的，那么可以通过这个宝藏左右最近的safecolumns离开；最后拿到的是最右边的情况也同理；

3. 对于第一行来说，若有宝藏，则获得最右边的宝藏后离开；所无宝藏，则通过离[1, 1]最近的safecolumn离开；

4. 对于其他行来说，最多可以有四种方式离开此行，最后一行不需要到达safecolumn，获得所有宝藏即可；

宝藏左右最近的safecolumn，可以通过binary search求得。

注意，若最左边的宝藏就在safecolumn上，则其左右最近的safecolumn都是此列。

#include <iostream>
#include <set>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;

typedef long long LL;

int findSafe(vector<int>& safes, int x){
    int l = , r = safes.size()-, ret;
    while(l <= r){
        int m = (l+r)>>;
        if(safes[m] == x)
            return m;
        if(safes[m] > x)
            r = m - ;
        else{
            ret = m;
            l = m + ;
        }
    }
    return ret;
}

int dist(int layer, int p1, int p2, vector<int>& leftmost, vector<int>& rightmost, vector<int>& safecol){
    if(safecol[p1] > safecol[p2])
        swap(p1, p2);
    int d = safecol[p2] - safecol[p1];
    if(rightmost[layer] > safecol[p2])
        d +=  * (rightmost[layer]-safecol[p2]);
    if(leftmost[layer] < safecol[p1])
        d +=  * (safecol[p1]-leftmost[layer]);
    return d;
}

int main(){
    int n, k, m, q;
    cin>>n>>m>>k>>q;
    vector<int> leftmost(n+, m+), rightmost(n+, ), safecol{};
    for(int i=; i<k; i++){
        int row, col;
        cin>>row>>col;
        leftmost[row] = min(leftmost[row], col);
        rightmost[row] = max(rightmost[row], col);
    }
    for(int i=; i<q; i++){
        int safe;
        cin>>safe;
        safecol.push_back(safe);
    }

    sort(safecol.begin(), safecol.end());

    while(leftmost[n] == m+) n--;

    if(n==){
        cout<<rightmost[]-<<endl;
        return ;
    }
    vector<LL> now_step{, ,  ,}, lst_step{, , , };
    vector<int> lst_gate{-, -, -, -};
    if(rightmost[] == ){
        int rsafe = findSafe(safecol, );
        if(safecol[rsafe] < )
            rsafe++;
        lst_gate[] = rsafe;
        lst_step[] = safecol[rsafe]-;
    }else{
        int lsafe = findSafe(safecol, rightmost[]);
        //cout<<rightmost[1]<<"*"<<lsafe<<endl;
        lst_gate[] = lsafe;
        lst_step[] = *rightmost[]-safecol[lsafe]-;
        //cout<<"l10:"<<lst_step[0]<<endl;
        if(safecol[lsafe]<rightmost[] && lsafe+ < safecol.size()){
            lst_gate[] = lsafe+;
            lst_step[] = safecol[lsafe+]-;
        }
    }

    for(int i=; i<n; i++){
        if(leftmost[i] == m+){
            for(int j=; j<; j++)
                lst_step[j]++;
            continue;
        }else{
            vector<int> now_gate{-, -, -, -};
            int g1 = findSafe(safecol, leftmost[i]);
            int g2 = findSafe(safecol, rightmost[i]);
            //cout<<g1<<" "<<g2<<endl;
            now_gate[] = g1;
            if(safecol[g1] < leftmost[i] && g1+ < safecol.size())
                now_gate[] = g1+;
            now_gate[] = g2;
            if(safecol[g2] < rightmost[i] && g2+ < safecol.size())
                now_gate[] = g2+;
            for(int j=; j<; j++){
                now_step[j] = (*1e5+) * (*1e5);
                for(int u=; u<; u++)
                    if(lst_gate[u]> && now_gate[j]>){
                        int d = +dist(i,now_gate[j], lst_gate[u], leftmost, rightmost, safecol);
                        //cout<<now_gate[j]<<" "<<lst_gate[u]<<endl;
                        //cout<<"d:"<<i<<" "<<d<<endl;
                        //cout<<"ld:"<<" "<<lst_step[u]<<endl;
                        now_step[j] = min(now_step[j], lst_step[u]+d);
                    }
            }
            lst_step = now_step;
            lst_gate = now_gate;
        }
    }
    LL ret = (*1e5+) * (*1e5);
    for(int u=; u<; u++)
        if(lst_gate[u] > ){
            int d = +rightmost[n]-leftmost[n]+min(abs(rightmost[n]-safecol[lst_gate[u]]), abs(leftmost[n]-safecol[lst_gate[u]]));
            //cout<<"d:"<<" "<<d<<endl;
            //cout<<"lst_step:"<<lst_step[u]<<endl;
            ret = min(ret, lst_step[u]+d);
        }
    printf("%I64d\n", ret);
    return ;
}