3.决策树ID3算法原理
1.决策树的作用
主要用于解决分类问题的一种算法
2.建立决策树的3中常用算法
1).ID3---》信息增益
2).c4.5--> 信息增益率
4).CART Gini系数
3.提出问题:
ID3算法中,选择根节点时为什么要使得信息增益最大的特征呢?
***************************后续内容均为更好的理解3中所提出的的问题展开****************************
4.ID3算法的理解
如何更好的理解决策树的建立原理呢:我想从下图的层次去理解决策树的原理
首先用倒序的方式来将问题细化如下图:

1).什么是自信息?
香农(shannon)给出的定义:信息是事务运动状态后存在方式不确定性的描述
对上述定义的理解:
引入图片(左图来源:西安电子科技大学老师信号论课程讲义图)
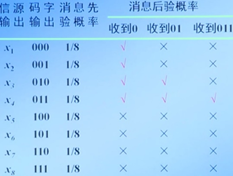
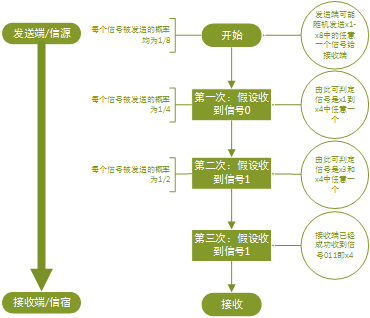
左图:
第一列:x1-x8表示的是发送端(信源)即将发送的信息的内容;
第二列:用3位的二进制数所唯一表征上述x1-x8
第三列:发送端随机发送任意一个信息内容的概率
通过右图我们可以发现,在信号传递过程中所体现出来的不确定性我们是可以通过概率的方式去量化表征的;
这样我们就可以预先假设不确定性和概率之前存在着一种量化的关系,可以做出如下的定义:在如下图所示的集合中,每一个事件x发生的不确定性可以定义为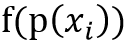
下面我们分析一下信息的不确定性的特点:
a.确定事件的不确定性为0,即f(1) = 0
b.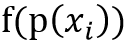 是单调减函数,即随着p(xi)的增大,f的值减小
是单调减函数,即随着p(xi)的增大,f的值减小
c.可加性,即a发生的不确定性为i,b发生的不确定性为j 那么a和b同时发生的不确定性为i + j
通过上述的假设的不确定性与概率之间的量化关系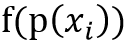 ,以及信号传递(或者说事件发生)过程中不确定性的特点,发现
,以及信号传递(或者说事件发生)过程中不确定性的特点,发现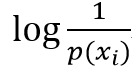 此种形式的函数满足如上假设以及特点
此种形式的函数满足如上假设以及特点
由此便有了信息的数学表达式为:
表达式1:事件xi的自信息-------------------------->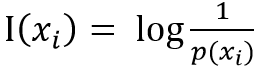
为什么称作自信息,暂且理解为只考虑自身的不确定性,后边的内容了解之后,大家就知道为甚这么叫了。
表达式2:事件xi的条件自信息------------------->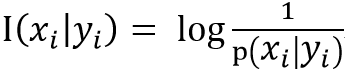
含义:事件yi发生的情况下,事件xi发生的不确定性的大小
表达式3:事件x的非平均互信息:------------->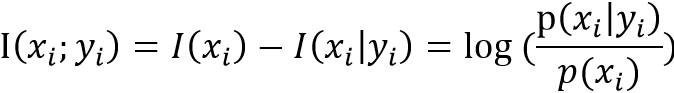
含义:观测某一事件后所得到的关于信源事件不确定性的大小;
分步骤理解:
第一步:y事件发生前x事件发生的可能性为I(x)
第二步:y事件发生后x事件发生的可能性为I(x|y)
第三步:两者的差值即就是观测y事件发生后所得到的关于x事件不确定性的大小
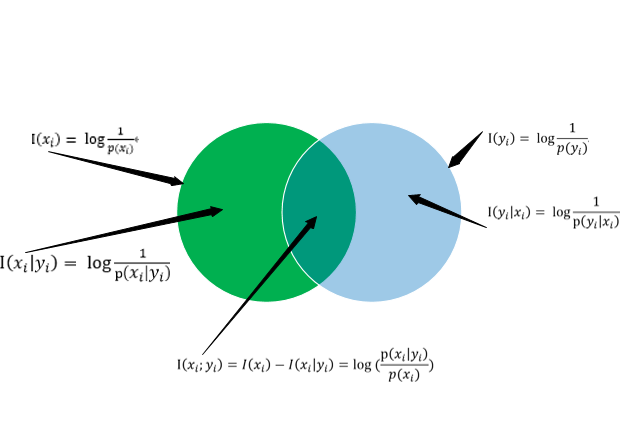
通过上图,我们可以更直观得到自信息,条件自信息,非平均互信息三者之间的关系;
******************************************************************************************
2).什么是信息熵?
在理解什么是信息的过程中,我们引入的都是单一事件,表征的均为单一事件的不确定性,那如何表征x1-x8这个集合的不确定性呢?这便引入了信息熵,来度量集合的平均不确定性,表达式如下:
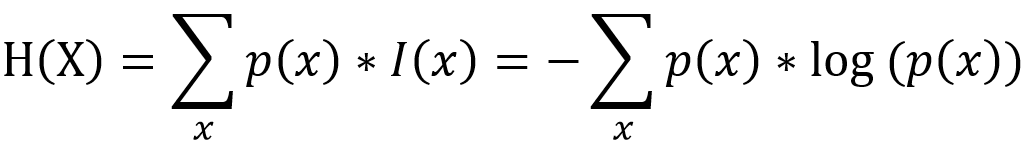
如何理解熵的与信息之间的关系:信息用来表征单一事件发生的不确定性,而熵是表征一个事件集合发射的平均不确定性,此处的平均实为加权平均
下面是几种熵的表达式:
表达式1:条件平均子信息(注意此时的x是一个集合)
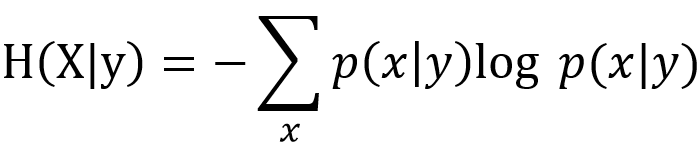
表达式2:条件熵
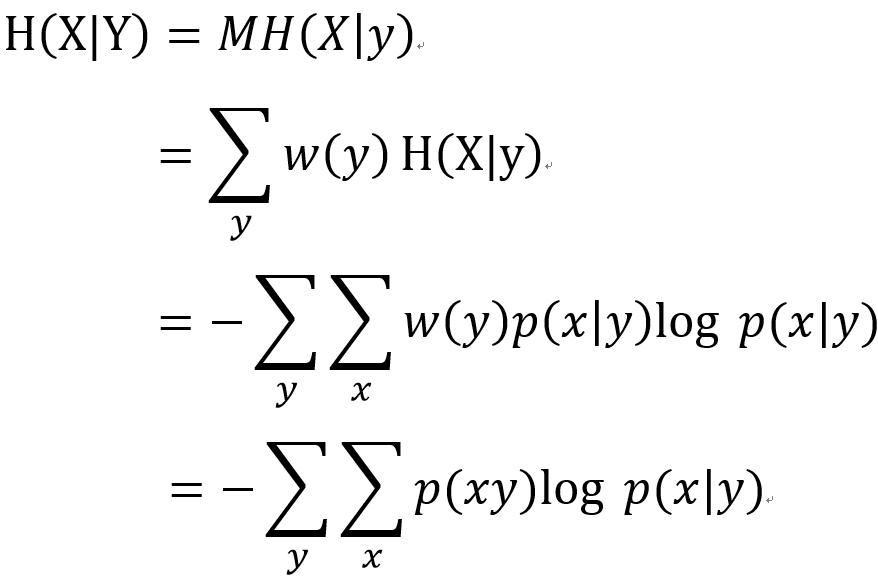
表达式3:平均互信息
定义1:特定事件y属于Y w(y)>0出现时所给出的关于集合{X,p(x)}中格式件的平均互信息的表达式:
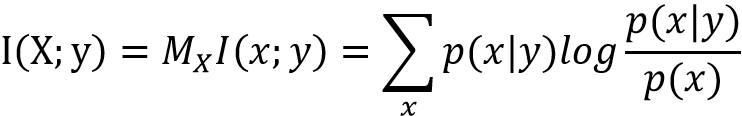
含义:观测某一事件后所得到的信源事件整体平均不确定性的大小
定义2:集合{XY,p(xy)}中随机变量I(x;y)的数学期望:
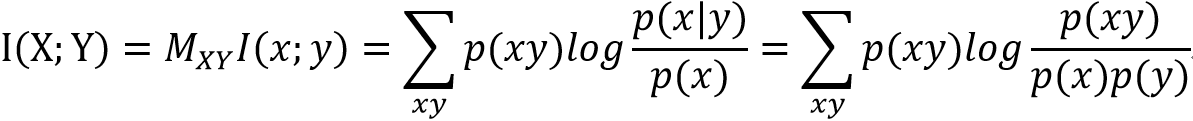
含义:观测集合整体后所得到的信源事件整体平均不确定性的大小
关系如下图:
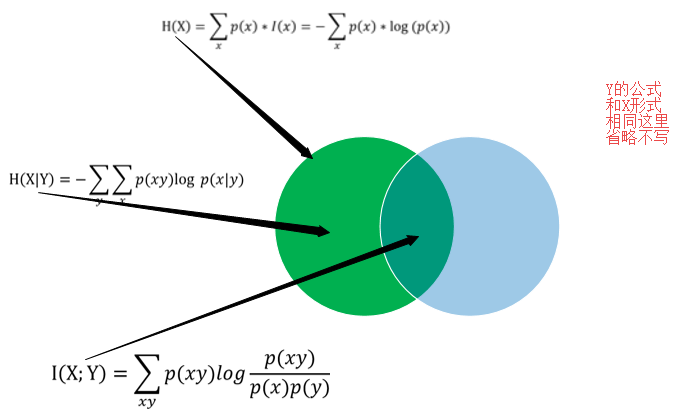
我们发现: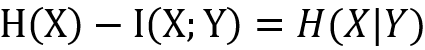
下面给出上述关系的证明:(此时就是信息增益的关系时)
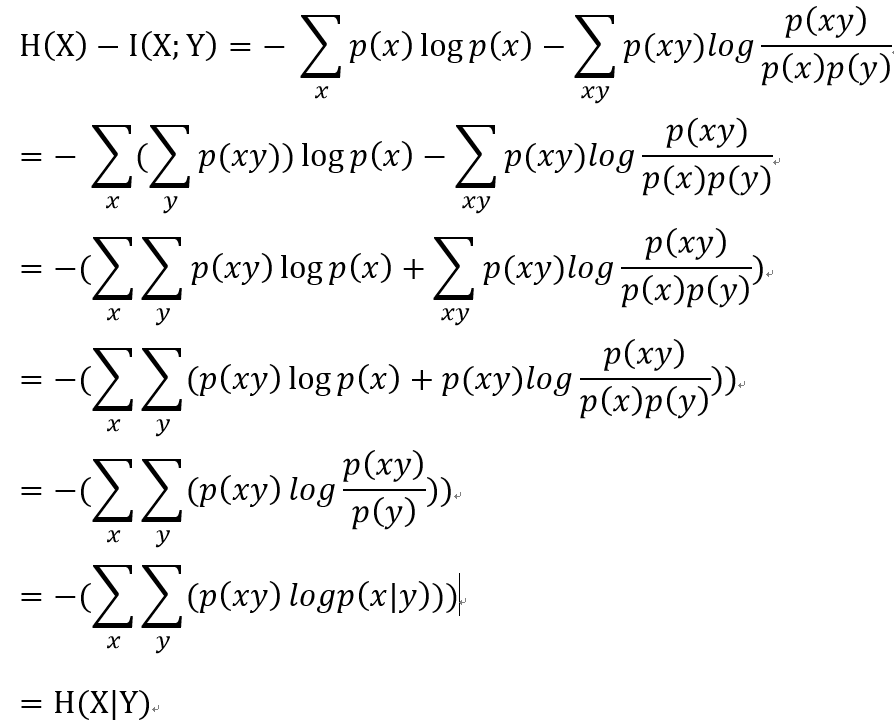
5.结论:
下面解决我们最初提出的问题即:ID3算法中,选择根节点时为什么要使得信息增益最大的特征呢?
首先明确我们在决策树中所提出的信息增益即就是平均互信息I(X;Y),含义如上文中蓝色字体所示,也可以理解为是Y事件集发生后,使得x发生的不确定性的减少程度
为什么要信息增益大呢?如下图所示当信息增益越大时,时件y发生后时间x的不确定性(即条件互信息)越来越小,这个正是我们所想要的;
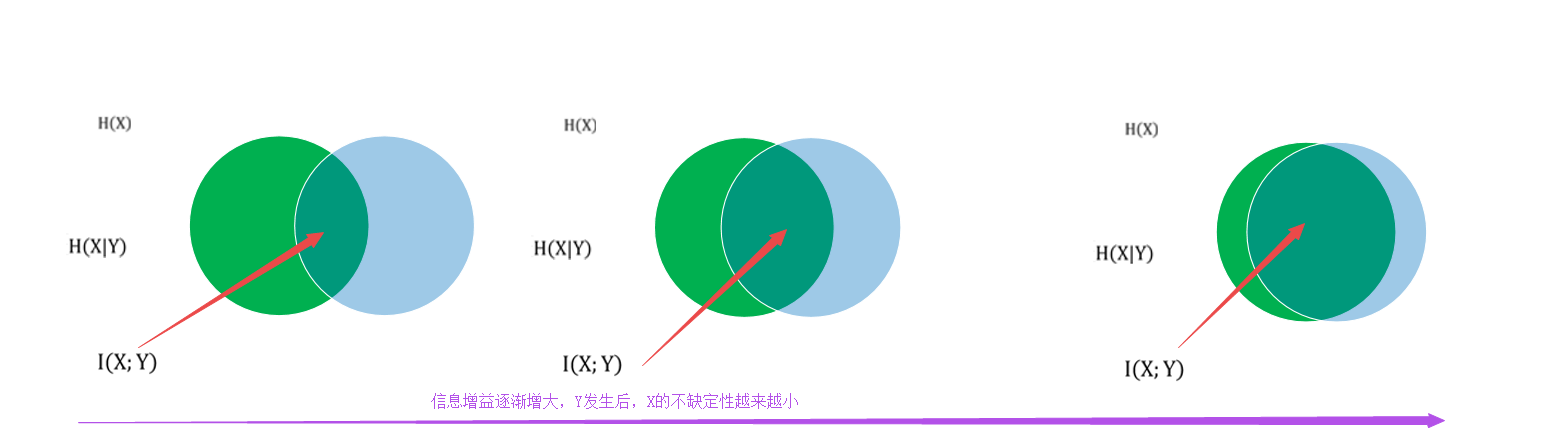
3.决策树ID3算法原理的更多相关文章
- 机器学习之决策树(ID3)算法与Python实现
机器学习之决策树(ID3)算法与Python实现 机器学习中,决策树是一个预测模型:他代表的是对象属性与对象值之间的一种映射关系.树中每个节点表示某个对象,而每个分叉路径则代表的某个可能的属性值,而每 ...
- 数据挖掘之决策树ID3算法(C#实现)
决策树是一种非常经典的分类器,它的作用原理有点类似于我们玩的猜谜游戏.比如猜一个动物: 问:这个动物是陆生动物吗? 答:是的. 问:这个动物有鳃吗? 答:没有. 这样的两个问题顺序就有些颠倒,因为一般 ...
- 决策树ID3算法[分类算法]
ID3分类算法的编码实现 <?php /* *决策树ID3算法(分类算法的实现) */ /* *求信息增益Grain(S1,S2) */ //-------------------------- ...
- 决策树---ID3算法(介绍及Python实现)
决策树---ID3算法 决策树: 以天气数据库的训练数据为例. Outlook Temperature Humidity Windy PlayGolf? sunny 85 85 FALSE no ...
- 02-21 决策树ID3算法
目录 决策树ID3算法 一.决策树ID3算法学习目标 二.决策树引入 三.决策树ID3算法详解 3.1 if-else和决策树 3.2 信息增益 四.决策树ID3算法流程 4.1 输入 4.2 输出 ...
- 决策树ID3算法的java实现(基本试用所有的ID3)
已知:流感训练数据集,预定义两个类别: 求:用ID3算法建立流感的属性描述决策树 流感训练数据集 No. 头痛 肌肉痛 体温 患流感 1 是(1) 是(1) 正常(0) 否(0) 2 是(1) 是(1 ...
- 【Machine Learning in Action --3】决策树ID3算法
1.简单概念描述 决策树的类型有很多,有CART.ID3和C4.5等,其中CART是基于基尼不纯度(Gini)的,这里不做详解,而ID3和C4.5都是基于信息熵的,它们两个得到的结果都是一样的,本次定 ...
- 决策树--ID3 算法(一)
Contents 1. 决策树的基本认识 2. ID3算法介绍 3. 信息熵与信息增益 4. ID3算法的C++实现 1. 决策树的基本认识 决策树是一种 ...
- 决策树ID3算法的java实现(基本适用所有的ID3)
已知:流感训练数据集,预定义两个类别: 求:用ID3算法建立流感的属性描述决策树 流感训练数据集 No. 头痛 肌肉痛 体温 患流感 1 是(1) 是(1) 正常(0) 否(0) 2 是(1) 是(1 ...
随机推荐
- python list 中extend()与append()区别
def changextend(str): "print string with extend" mylist.extend([40,50,60]); print(mylist) ...
- Dubbo消费方服务调用过程源码分析
参考:dubbo消费方服务调用过程源码分析dubbo基于spring的构建分析Dubbo概述--调用过程dubbo 请求调用过程分析dubbo集群容错机制代码分析1dubbo集群容错策略的代码分析2d ...
- 剑指offer-和为S的两个数字-知识迁移能力-python
题目描述 输入一个递增排序的数组和一个数字S,在数组中查找两个数,使得他们的和正好是S,如果有多对数字的和等于S,输出两个数的乘积最小的. 输出描述: 对应每个测试案例,输出两个数,小的先输出. 思路 ...
- 淘宝flexible.js的使用
首先大家最关注的怎么使用,原理不原理是后面的事 比如设计稿量来的宽度是100px 那么我们布局的时候,就这么写{width:1.3333rem},1.3333rem是由100/75算出来的,以此类推2 ...
- Django框架——进阶之AJAX
<script>$("#b1").on("click", function () { // 点击 id是b1的按钮要做的事儿 var i1 = $( ...
- 并发编程系列:Java线程池的使用方式,核心运行原理、以及注意事项
并发编程系列: 高并发编程系列:4种常用Java线程锁的特点,性能比较.使用场景 线程池的缘由 java中为了提高并发度,可以使用多线程共同执行,但是如果有大量线程短时间之内被创建和销毁,会占用大量的 ...
- php函数之strtr和str_replace的区别
php字符串替换函数 strtr()有两种用法: strtr(string,from,to) 或者strtr(string,array) 首先针对strtr函数第一种方式: 我们看看下面的举例: &l ...
- 安全专家发现GE Multilin SR的一个关键漏洞对全球电网构成严重威胁。
A team of researchers from New York University has found a serious vulnerability in some of GE Multi ...
- Linux系统文件系统及文件基础篇
学习Linux,重难点在于掌握不同类别的文件系统及其作用.通过对Linux系统的安装,我们首先来了解下Linux系统里各个目录文件夹下的大致功能:主要的目录树的有/./root./home./usr. ...
- java8学习之自定义收集器深度剖析与并行流陷阱
自定义收集器深度剖析: 在上次[http://www.cnblogs.com/webor2006/p/8342427.html]中咱们自定义了一个收集器,这对如何使用收集器Collector是极有帮助 ...
