2020 OO 第一单元总结表达式求导

title: BUAA-OO 第一单元总结

date: 2020-03-19 20:53:41

tags: OO

categories: 学习

OO第一单元通过三次递进式的作业让我们实现表达式求导，在这几次作业中我也有很多收获。下面就回顾一下前三次作业中存在的问题。

在个人看来，表达式求导的难点主要有三部分——对输入的处理、表达式的存储结构以及化简。这三次作业我所采用的表达式存储结构都不相同，不过重构的速度还是比较快的（安慰自己）。

第一次作业

在第一次作业中，我的程序总体架构为提取幂函数为Poly对象，建立Polynomial类解析表达式创建幂函数对象，在主类Derivative中进行部分性能优化工作。

① 程序结构分析

UML类图：

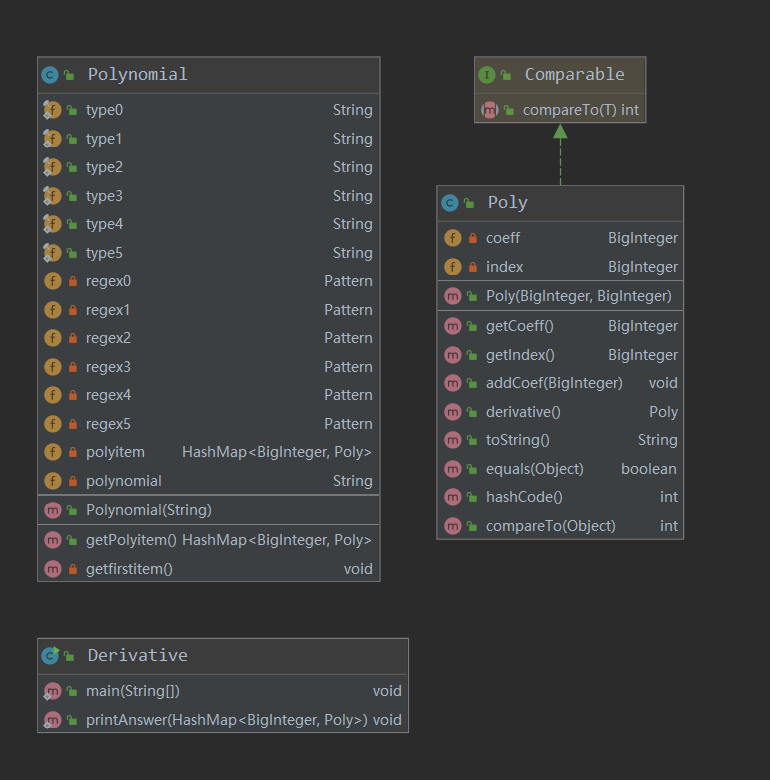
第一次作业的幂函数因子较为简单，代码中仅提炼出Poly对象，并在其内部实现求导方法。

Method复杂度：

Method	ev(G)	iv(G)	v(G)
Derivative.main(String[])	1	1	1
Derivative.printAnswer(HashMap<BigInteger, Poly>)	4	5	7
Poly.Poly(BigInteger,BigInteger)	1	1	1
Poly.addCoef(BigInteger)	1	1	1
Poly.compareTo(Object)	1	1	1
Poly.derivative()	1	2	2
Poly.equals(Object)	2	2	2
Poly.getCoeff()	1	1	1
Poly.getIndex()	1	1	1
Poly.hashCode()	1	1	1
Poly.toString()	1	11	12
Polynomial.Polynomial(String)	1	1	1
Polynomial.getPolyitem()	1	2	2
Polynomial.getfirstitem()	1	9	10

第一次作业中，化简主要在主类Derivative的printAnswer()方法（将第一个正项优先输出）和Poly类的toString()方法中，printAnswer()涉及对表达式的遍历，基本复杂性高；toString()则包含大量条件语句，多次调用了BigInteger中的方法，循环依赖性高。而表达式解析我采用的是正则+状态机的策略（这个策略三次作业均沿用，感觉还是很舒服的），在getfirstitem()中处理不同类型输入并归一化，代码较为复杂。

② 程序Bug分析

第一次作业在强测、互测中均未出现Bug。

③ 互测采用策略

互测时我采用的策略是“补刀”。我先是用简单的自动测试程序跑了下房间内成员的代码，不过貌似没有出现问题；然而圣杯战争发生了转机——Rider竟然拿下了一血！

于是我一一检查其他成员的代码，发现Berserker的正则存在问题：在正则中匹配的是“[+|-]{0,2}(\\d*.)?x(..[+|-]?\\d+)?”，其中的“.”可匹配任意字符，就会错误解析表达式。

第一次互测时认真读了屋内其他同学的代码，感觉还是很有收获的。之后两次大部分都读不下去，可读性实在是让人肝疼……放到评测姬里自生自灭吧！另外这次互测也让我意识到了高工同学的可怕之处（误），全屋子就这一个Bug，大佬换着花样hack……卷卷更健康。

④ 对象创建模式

在第一次作业中，我并没有应用对象创建模式，表达式解析就顺便new了新因子，Polynomial类的紧耦合比较严重。

第二次作业

第二次作业增加了三角函数因子，这个时候我也偷偷看了一下去年的第三次作业题目，新增加的嵌套对于表达式的化简无疑是不小的挑战。所以在规划第二次作业的总体架构时，我就面临着一个选择——是要建立终将在第三次作业重构的四元组项；还是要采用“表达式-项-因子”三层结构，为第三次作业留好迭代的空间？

经过一番挣扎（其实并没有，因为我还不会写三层结构），我选择了势必带来重构的四元组形式，也就是将表达式的每一项以“coeff*x**powindex*sin(x)**sinindex*cos(x)**cosindex”的形式存储，这样处理方式就和第一次作业基本一致。在基本架构沿用第一次作业的情况下，第二次作业给我最大的挑战反而是三角函数的化简，我的化简类Simplify的行数是最多的。

① 程序结构分析

UML类图：

架构基本沿用第一次作业，UML也差不多，不过这次的简化更复杂一些。

Method复杂度：

Method	ev(G)	iv(G)	v(G)
DeriPrinter.DeriPrinter(HashMap<String, MutiItem>)	1	7	7
DeriPrinter.getAnswer(HashMap<String, MutiItem>)	4	5	7
DeriPrinter.printAnswer()	1	2	2
Item.Item(BigInteger,BigInteger,BigInteger)	1	1	1
Item.compareTo(Object)	3	3	3
Item.equals(Object)	2	4	4
Item.getCosin()	1	1	1
Item.getPowin()	1	1	1
Item.getSinin()	1	1	1
Item.hashCode()	1	1	1
Item.toString()	1	5	8
MainClass.main(String[])	1	1	1
MutiItem.MutiItem(BigInteger,BigInteger,BigInteger,BigInteger)	1	1	1
MutiItem.MutiItem(BigInteger,Item)	1	1	1
MutiItem.addCoeff(BigInteger)	1	1	1
MutiItem.compareTo(Object)	1	1	1
MutiItem.derivate()	1	5	5
MutiItem.equals(Object)	2	2	2
MutiItem.getCoeff()	1	1	1
MutiItem.getCosin()	1	1	1
MutiItem.getIdentity()	1	1	1
MutiItem.getItem()	1	1	1
MutiItem.getPowin()	1	1	1
MutiItem.getSinin()	1	1	1
MutiItem.hashCode()	1	1	1
MutiItem.toString()	1	5	5
ParseExp.MutiItemSign()	2	3	4
ParseExp.ParseExp(String)	1	5	6
ParseExp.WrongFormat(String)	1	1	1
ParseExp.getExpression()	1	2	2
ParseExp.getFirstitem()	3	13	14
Simplify.Simplify(HashMap<String, MutiItem>)	1	2	2
Simplify.exitmatch(BigInteger,Item,Item,Item,HashMap<Item, BigInteger>)	2	3	4
Simplify.searchcos(HashMap<Item, BigInteger>)	4	6	9
Simplify.simplify()	1	3	4

由于一开始并没有明确的化简思路，在第一遍实现了基本求导功能的代码通过中测之后，我为了实现化简功能，又对代码内类的结构做了很多修改，在这一过程中，尽管我确实用类将表达式中的Item与MulItem做了封装，但我却胡乱修改内部方法，这并不符合面向对象的思想，也导致最后代码可读性极差，也为互测时被发现的Bug埋下了祸根。具体表现到MetricReloaded的分析上，就是ParseExp类的getFirstitem()依然是复杂度重灾区，没有采用工厂模式也使得它与其他类的依赖极为严重，优化输出的内容依然有很高的基本复杂性。

② 程序Bug分析

强测中获得性能分为16.545/20，在处理表达式化简时，我所采用的是暴力搜索的方式，每次搜索到可以合并的项就将其合并，然后进行重新搜索。

这种方法显然只能找到一个极优解，却不能找到最优解，表达式项存储顺序对结果也有很大影响。一种更加可行的方式是采用深度优先搜索，不过当时并没有想出具体的实现方法，只好作罢。

互测时被找出来一个Bug，同时发现Berserker的一个Bug（狂战士日常躺枪）。而我的Bug是HashMap的Key写错，在生成MulItem的Key时，我采用的是将指数拼接为String的方式，在指数较大时，可能会导致不同项被当作同一项存入HashMap中，造成求导错误。

修改也很简单，只需要在生成String的时候给不同指数加个分隔符就好了——

 public MutiItem(BigInteger a, BigInteger b, BigInteger c, BigInteger d) {
     this.coeff = a;
     this.item = new Item(b, c, d);
     // before: identity = "" + b + c + d;
     identity = "" + b + "." + c + "." + d;
 }

可以发现这里我的MutiItem的构造方法是非常混乱的，不过没有发现这么明显的Bug，一方面就是混乱的优化带来的副作用；另一方面也是因为这样的数据出现几率确实很小，同屋里也只有一个同学发现了这个Bug（我后来和hack我的同学交流了下，果然是长时间跑随机自动测试程序才找到的……）

③ 互测采用策略

在这次互测是采用对拍+手动构造样例+Python生成随机数据自动评测的方式。屋内除我只有一个Bug，大家很快找到之后也比较佛系。

互测中阅读了同屋子大佬处理简化的DFS，确实厉害；另外还拜读了另一个房间Alterego的架构，类似Sympy的表达式结构简直叫人拍案叫绝，计算方式优美，让我看到了什么是真正的封装、多态、继承，也有更多信心去面对第三次作业。（不过听说在那个屋Alterego被hack的很惨，悲）

④ 对象创建模式

在第二次作业中，由于使用的是和第一次作业类似的四元组项，我依然没有应用对象创建模式，表达式解析里又new了新因子，紧耦合依然严重。这在第三次作业中有一定改善。

第三次作业

前两次作业都没有对表达式进行结构化处理，导致了第三次作业表达式的存储结构必须大改。

好在表达式求导的三大难点——对输入的处理、表达式的存储结构以及化简，这次都处理得比较好——

对输入的处理上，有了前两次作业中采用的正则表达式加有限状态机读入的经验，修改很快；
表达式的存储结构上吸取了Alterego的架构（感谢Alterego！！！！），在进行重构的时候思路比较清晰，避免了第二次作业惨剧的重演；
化简上，层次化的表达式存储方式发挥出了它的优越性，通过统一的接口进行因子类型的转换，效果好；

在第三次作业我也首次采用了Package来管理类，也是一个小进步。

① 程序结构分析

UML类图：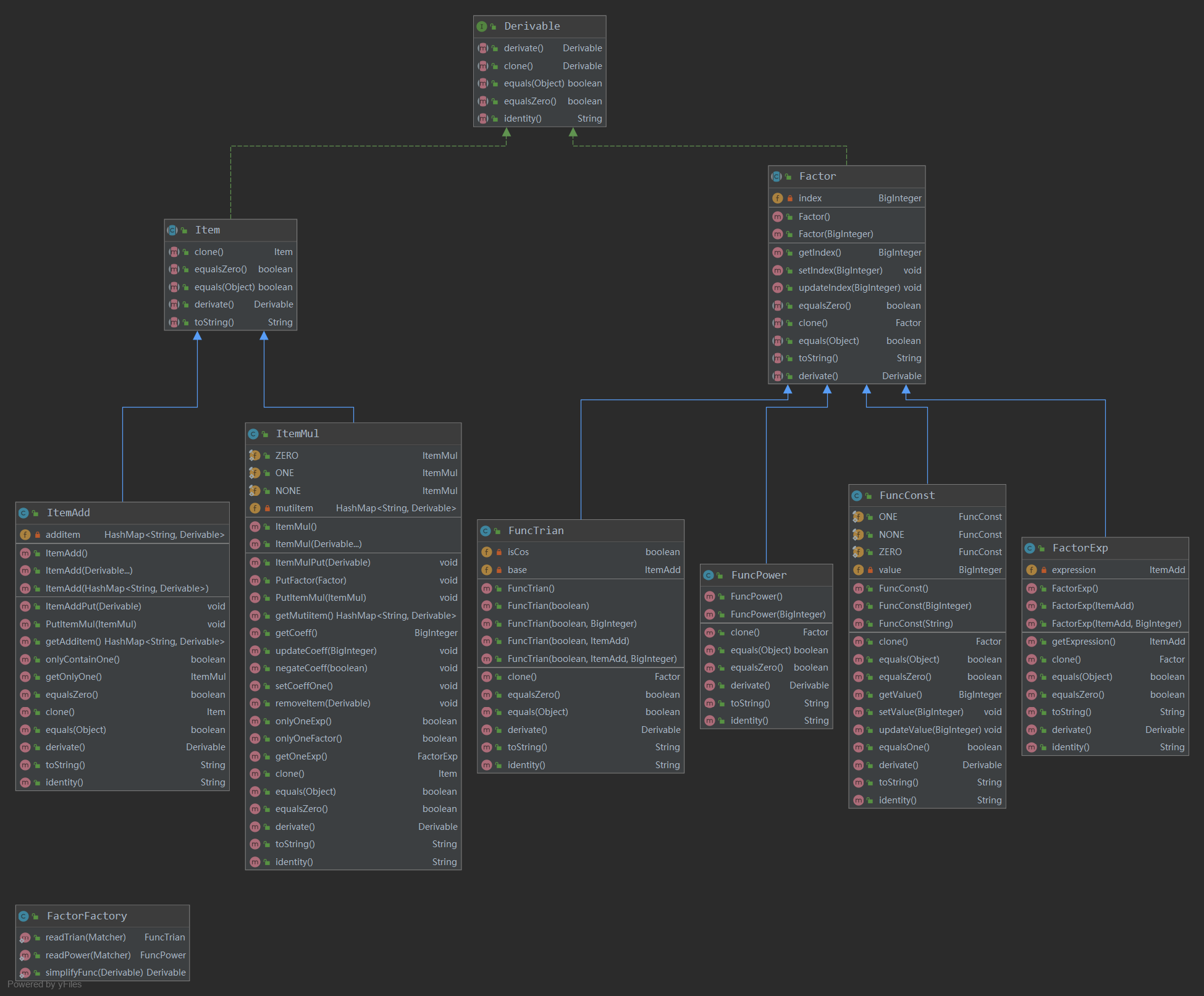

表达式解析为ItemAdd和ItemMul两层（内部有大量简化方法），以及因子，都实现了求导接口，以抽象类约束。

这一次的类图很乱，主要原因还是在于表达式也可以作为一个因子嵌套进三角函数中，类之间的相互调用也比较明显。

Method复杂度：

Method	ev(G)	iv(G)	v(G)
homework.MainClass.main(String[])	1	2	2
homework.expression.ExpFunction.Exception.Exception(String)	1	1	1
homework.expression.ExpFunction.deleteSpace(String)	3	7	10
homework.expression.ExpFunction.matchParentheses(String,int)	6	6	7
homework.expression.ExpFunction.readIndex(String)	2	1	2
homework.expression.ExpFunction.simplifyExpParentheses(String)	9	11	14
homework.expression.ExpFunction.simplifyParentheses(String,int[])	1	1	8
homework.expression.ExpFunction.simplifySign(String)	4	3	4
homework.expression.ExpParser.Exception.Exception(String)	1	1	1
homework.expression.ExpParser.ExpParser(String)	3	2	3
homework.expression.ExpParser.getItemAdd(String,boolean)	5	6	9
homework.expression.ExpParser.getItemMul(String)	4	3	5
homework.expression.ExpParser.matchParentheses()	7	4	8
homework.expression.ExpParser.readOneItem(String)	6	9	12
homework.expression.ExpParser.spliter()	1	1	1
homework.expression.ExpSimplify.ExpSimplify(Derivable)	1	2	2
homework.expression.ExpSimplify.OnlyOneDiff(Derivable,Derivable)	9	17	26
homework.expression.ExpSimplify.getDiff(boolean,int,int,ItemMul,ItemMul)	1	4	6
homework.expression.ExpSimplify.searchSimplify(ItemAdd)	4	4	4
homework.expression.ExpSimplify.simplify()	2	2	4
homework.polyitem.factor.Factor.Factor()	1	1	1
homework.polyitem.factor.Factor.Factor(BigInteger)	1	1	1
homework.polyitem.factor.Factor.getIndex()	1	1	1
homework.polyitem.factor.Factor.setIndex(BigInteger)	1	1	1
homework.polyitem.factor.Factor.updateIndex(BigInteger)	1	1	1
homework.polyitem.factor.FactorExp.FactorExp()	1	1	1
homework.polyitem.factor.FactorExp.FactorExp(ItemAdd)	1	1	1
homework.polyitem.factor.FactorExp.FactorExp(ItemAdd,BigInteger)	1	1	1
homework.polyitem.factor.FactorExp.clone()	1	1	1
homework.polyitem.factor.FactorExp.derivate()	4	4	5
homework.polyitem.factor.FactorExp.equals(Object)	3	3	4
homework.polyitem.factor.FactorExp.equalsZero()	1	1	1
homework.polyitem.factor.FactorExp.getExpression()	1	1	1
homework.polyitem.factor.FactorExp.identity()	1	1	1
homework.polyitem.factor.FactorExp.toString()	1	4	4
homework.polyitem.factor.FactorFactory.readPower(Matcher)	1	2	2
homework.polyitem.factor.FactorFactory.readTrian(Matcher)	1	2	3
homework.polyitem.factor.FactorFactory.simplifyFunc(Derivable)	2	4	5
homework.polyitem.factor.FuncConst.FuncConst()	1	1	1
homework.polyitem.factor.FuncConst.FuncConst(BigInteger)	1	1	1
homework.polyitem.factor.FuncConst.FuncConst(String)	1	1	1
homework.polyitem.factor.FuncConst.clone()	1	1	1
homework.polyitem.factor.FuncConst.derivate()	1	1	1
homework.polyitem.factor.FuncConst.equals(Object)	2	2	2
homework.polyitem.factor.FuncConst.equalsOne()	1	1	1
homework.polyitem.factor.FuncConst.equalsZero()	1	1	1
homework.polyitem.factor.FuncConst.getValue()	1	1	1
homework.polyitem.factor.FuncConst.identity()	1	1	1
homework.polyitem.factor.FuncConst.setValue(BigInteger)	1	1	1
homework.polyitem.factor.FuncConst.toString()	1	1	1
homework.polyitem.factor.FuncConst.updateValue(BigInteger)	1	1	1
homework.polyitem.factor.FuncPower.FuncPower()	1	1	1
homework.polyitem.factor.FuncPower.FuncPower(BigInteger)	1	1	1
homework.polyitem.factor.FuncPower.clone()	1	1	1
homework.polyitem.factor.FuncPower.derivate()	1	1	2
homework.polyitem.factor.FuncPower.equals(Object)	2	2	2
homework.polyitem.factor.FuncPower.equalsZero()	1	1	1
homework.polyitem.factor.FuncPower.identity()	1	1	1
homework.polyitem.factor.FuncPower.toString()	1	1	2
homework.polyitem.factor.FuncTrian.FuncTrian()	1	1	1
homework.polyitem.factor.FuncTrian.FuncTrian(boolean)	1	1	1
homework.polyitem.factor.FuncTrian.FuncTrian(boolean,BigInteger)	1	1	1
homework.polyitem.factor.FuncTrian.FuncTrian(boolean,ItemAdd)	1	1	1
homework.polyitem.factor.FuncTrian.FuncTrian(boolean,ItemAdd,BigInteger)	1	1	1
homework.polyitem.factor.FuncTrian.clone()	1	2	2
homework.polyitem.factor.FuncTrian.derivate()	4	4	6
homework.polyitem.factor.FuncTrian.equals(Object)	6	4	8
homework.polyitem.factor.FuncTrian.equalsZero()	3	3	4
homework.polyitem.factor.FuncTrian.identity()	1	4	5
homework.polyitem.factor.FuncTrian.toString()	1	2	3
homework.polyitem.item.ItemAdd.ItemAdd()	1	1	1
homework.polyitem.item.ItemAdd.ItemAdd(Derivable...)	1	3	3
homework.polyitem.item.ItemAdd.ItemAdd(HashMap<String, Derivable>)	1	1	1
homework.polyitem.item.ItemAdd.ItemAddPut(Derivable)	1	4	4
homework.polyitem.item.ItemAdd.PutItemMul(ItemMul)	1	5	5
homework.polyitem.item.ItemAdd.clone()	1	2	2
homework.polyitem.item.ItemAdd.derivate()	2	2	3
homework.polyitem.item.ItemAdd.equals(Object)	3	2	3
homework.polyitem.item.ItemAdd.equalsZero()	3	2	3
homework.polyitem.item.ItemAdd.getAdditem()	1	1	1
homework.polyitem.item.ItemAdd.getOnlyOne()	4	2	4
homework.polyitem.item.ItemAdd.identity()	1	1	1
homework.polyitem.item.ItemAdd.onlyContainOne()	1	1	1
homework.polyitem.item.ItemAdd.toString()	6	5	7
homework.polyitem.item.ItemMul.ItemMul()	1	1	1
homework.polyitem.item.ItemMul.ItemMul(Derivable...)	3	3	3
homework.polyitem.item.ItemMul.ItemMulPut(Derivable)	3	5	6
homework.polyitem.item.ItemMul.PutFactor(Factor)	6	10	10
homework.polyitem.item.ItemMul.PutItemMul(ItemMul)	1	2	2
homework.polyitem.item.ItemMul.clone()	1	2	2
homework.polyitem.item.ItemMul.derivate()	6	2	7
homework.polyitem.item.ItemMul.equals(Object)	3	2	3
homework.polyitem.item.ItemMul.equalsZero()	3	2	3
homework.polyitem.item.ItemMul.getCoeff()	2	2	2
homework.polyitem.item.ItemMul.getMutiitem()	1	1	1
homework.polyitem.item.ItemMul.getOneExp()	5	2	5
homework.polyitem.item.ItemMul.identity()	2	3	4
homework.polyitem.item.ItemMul.negateCoeff(boolean)	1	2	2
homework.polyitem.item.ItemMul.onlyOneExp()	3	3	7
homework.polyitem.item.ItemMul.onlyOneFactor()	4	3	7
homework.polyitem.item.ItemMul.removeItem(Derivable)	1	2	2
homework.polyitem.item.ItemMul.setCoeffOne()	1	1	1
homework.polyitem.item.ItemMul.toString()	1	7	7
homework.polyitem.item.ItemMul.updateCoeff(BigInteger)	1	1	1

MetricReloaded分析程序复杂度更加病态了，大量方法的结构化程度存在问题，并且集中在与化简有关的方法中。表达式解析中的readOneItem()方法三项均超标，虽然我已经进行了采用了一部分的工厂模式、将正则表达式存入单独的类中以被调用的解耦合的努力。

Package复杂度：

Package	v(G)avg	v(G)tot
homework	2	2
homework.expression	6.68	127
homework.polyitem.factor	1.86	93
homework.polyitem.item	3.38	115

通过分包，将几大功能区分开（不过这次看到20%的性能分，增加了暴力搜索提取公因式的简化方法，还是放在Exp处理中，所以耦合度也有点高）。

② 程序Bug分析

“OO中最惨的，不是被同屋hack了50个同质Bug，而是在截止提交的下一秒意识到了自己的Bug”

——沃茨基·硕德

在第三次作业中，我为了简化做了不少工作，也用随机数据自动测试程序做了大量的检验。然而就在周六晚上截止提交后的几秒，我突然意识到我的输出是有问题的——对于表达式因子，我将其设置为继承了Factor类，同样拥有指数Index属性，在输出时，采用的是和幂函数、三角函数一样的输出方式——“(exp)**index”，但在输入时表达式因子是不允许有指数的，因此属于WF。但对于Sympy，表达式的格式限定很宽松，通过计算并不能找到错误。

那能咋办……周六晚上看番转移注意力，周日在互测中尽可能挽回损失……最后发现强测没有出现这种输出，但互测时被同屋两名Servent发现了这个Bug。好在修复工作也比较简单，实在是侥幸。

③ 互测采用策略

在这次互测依然是采用对拍（对军宝具）+手动构造样例（我自己构造了可能会TLE的样例，也分享到了群里）+Python生成随机数据自动评测的方式。

在这次对Python生成随机数据做了优化，比如Caster在指数为0时会出现各种吊诡的错误，然而互测限定指数>0，于是我将对Caster的随机数据设为指数始终>0，其他成员照旧，避免了反复查看不能hack的Bug带来的失落感。

最后稍微吐槽一下“不优化就不会Die”，在这次互测中，房间内8名成员，4名优化输出4名不优化，最后出Bug的都是那4名优化输出的……其中Berserker还会在表达式嵌套过多时陷入死循环，截止至本文发稿时已被修好。

④ 对象创建模式

在这次的作业中终于用到了工厂模式！虽然原因是表达式解析方法太长，不得不将生成项的代码独立开来。不过我也只用工厂模式处理了幂函数、不含嵌套因子的三角函数、常数，含嵌套因子的三角函数的生成与我的状态机密切相关，难以抽象出来，这也是我的架构中的不足。

心得体会

在寒假的时候，我曾看到知乎上@HansBug学长关于OO课程改革的回答，而通过这一个多月的实际体验，OO给我的感受还是很赞的，通过互测阅读同学代码、与舍友们的交流（感谢@VOIDMalkuth！！！）、水讨论区以及学习理论课，收获很大。

第一单元也只是从面向过程到面向对象的过渡篇章，通过这次反思，我也发现了过去几次代码中自己结构较为不合理的部分，希望能够在接下来多线程等知识的学习中进一步改善。