SVM中的软间隔最大化与硬间隔最大化

参考文献：https://blog.csdn.net/Dominic_S/article/details/83002153

1.硬间隔最大化

对于以上的KKT条件可以看出，对于任意的训练样本总有ai=0或者yif(xi) - 1=0即yif(xi) = 1
1）当ai=0时，代入最终的模型可得：f(x)=b，样本对模型没有贡献
2）当ai>0时，则必有yif(xi) = 1，注意这个表达式，代表的是所对应的样本刚好位于最大间隔边界上，是一个支持向量，这就引出一个SVM的重要性质：训练完成后，大部分的训练样本都不需要保留，最终的模型仅与支持向量有关。

2.软间隔最大化

如果数据加入了少数噪声点，而模型为了迁就这几个噪声点改变决策平面，即使让数据仍然线性可分，但是边际会大大缩小，这样模型的准确率虽然提高了，但是泛化误差却升高了，这也是得不偿失的。

或者有一些数据，线性不可分，或者说线性可分状况下训练准确率不能达到100%，即无法让训练误差为0。

此时此刻，我们需要让决策边界能够忍受一小部分训练误差，而不能单纯地寻求最大边际了。因为边际越大被分错的样本也就会越多，因此我们需要找出一个”最大边际“与”被分错的样本数量“之间的平衡，引入一个松弛系数ζ。

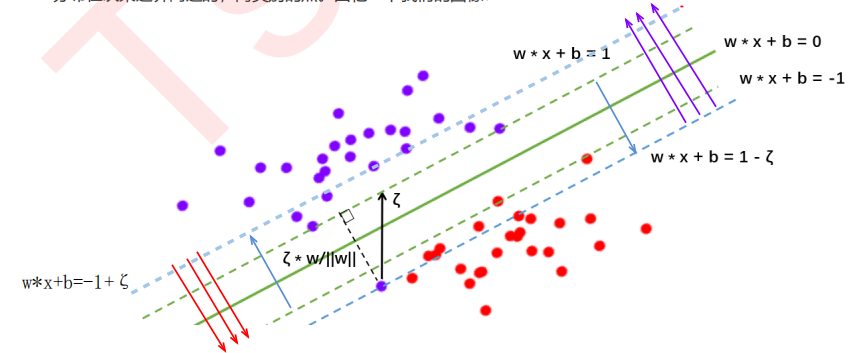
在硬间隔中：决策平面是绿色实线，约束条件是要保证两类样本点分别位于两条绿色虚线的两侧，所有样本点都被正确分类。

在软间隔中：决策平面是绿色实线，约束条件变为蓝色虚线，且红色样本点在红色箭头一侧即可，紫色样本点在紫色箭头一侧即可。

由于ζ是松弛量，即偏离绿色虚线的函数距离（绿色虚线到决策平面的距离为1），松弛量越大，表示样本点离绿色虚线越远，如果松弛量大于1，那么表示样本越过决策平面，即允许该样本点被分错。模型允许分类错误的样本数越多，模型精确性越低。因此需要对所有样本的松弛量之和进行控制，因此将所有样本量之和加入目标函数。

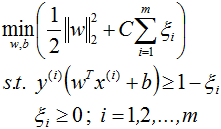
C表示的是在目标函数中松弛量的权重，C越大表示最小化时更多的考虑最小化ζ，即允许模型错分的样本越少，C值的给定需要调参。

同硬间隔最大化SVM，构造软间隔最大化的约束问题对应的Lagrange函数如下：

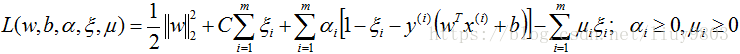
优化目标函数为： 

对偶问题为：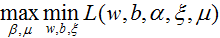

带入对偶函数得：

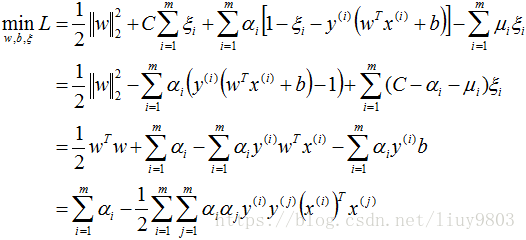
再对上式求α的极大值，即得对偶问题：

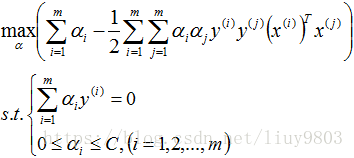
此处的约束条件由上面求导的2、3式可得。

软间隔SVM的KKT条件：

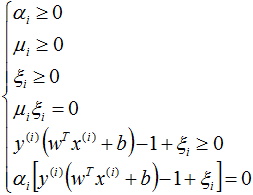
根据KKT条件中的对偶互补条件 αi(yi(wTxi+b)-1+ξi)=0 可知αi>0（即ai≠0）的样本为支持向量，在间隔边界上、间隔边界(yi(w*xi+b)=1)与决策超平面之间、或者在超平面误分一侧的向量都有可能是支持向量，因为软间隔模型中每个样本的αi、ξi不同，而αi、ξi不同的取值，样本就有可能落在不同的区域：

（1）αi<C,则μi>0，ξi=0，支持向量xi恰好落在间隔边界上；

（2）αi=C，则μi=0，则ζ≠0

　　　　　　0<ξi<1，则分类正确，xi在间隔边界与决策超平面之间；

　　　   ξi=1，则xi在决策超平面上；

　　　　　　ξi>1，则xi位于决策超平面误分一侧。

求得的每个样本点的α和ζ都不同，因此那条有松弛量的蓝色虚线超平面只是一个抽象概念，是不存在的，因为各个样本的松弛量都不同，C只是对总体样本的松弛量（即误差进行控制）。

支持向量是满足yi(w*xi+b)=1-ζi这个式子的样本，因为每个样本的ζi不同因此支持向量构不成线。间隔边界yi(w*xi+b)=1还在原来的地方。

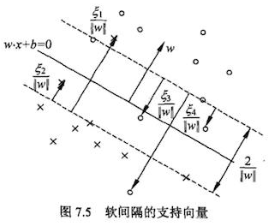
图中箭头所指的样本点都可以是支持向量。

如果给定的惩罚项系数C越小，在模型构建的时候就允许存在越多分类错误的样本，也就是表示此时模型的准确率比较低；如果给定的C越大，表示在模型构建的时候，允许分类错误的样本越少，也就表示此时模型的准确率比较高。