洛谷 P2114 [NOI2014]起床困难综合症 解题报告

P2114 [NOI2014]起床困难综合症

题目描述

21世纪，许多人得了一种奇怪的病：起床困难综合症，其临床表现为：起床难，起床后精神不佳。作为一名青春阳光好少年，atm一直坚持与起床困难综合症作斗争。通过研究相关文献，他找到了该病的发病原因： 在深邃的太平洋海底中，出现了一条名为drd的巨龙，它掌握着睡眠之精髓，能随意延长大家的睡眠时间。 正是由于drd的活动，起床困难综合症愈演愈烈， 以惊人的速度在世界上传播。为了彻底消灭这种病，atm决定前往海底，消灭这条恶龙。历经千辛万苦，atm终于来到了drd所在的地方，准备与其展开艰苦卓绝的战斗。drd有着十分特殊的技能，他的防御战线能够使用一定的运算来改变他受到的伤害。具体说来，drd的防御战线由n扇防御门组成。每扇防御门包括一个运算op和一个参数t，其中运算一定是OR,XOR,AND中的一种，参数则一定为非负整数。如果还未通过防御门时攻击力为x，则其通过这扇防御门后攻击力将变为x op t。最终drd受到的伤害为对方初始攻击力x依次经过所有n扇防御门后转变得到的攻击力。

由于atm水平有限，他的初始攻击力只能为0到m之间的一个整数（即他的初始攻击力只能在 0, 1, … , m中任选，但在通过防御门之后的攻击力不受m的限制）。为了节省体力，他希望通过选择合适的初始攻击力使得他的攻击能让drd受到最大的伤害，请你帮他计算一下，他的一次攻击最多能使drd受到多少伤害。

输入输出格式

输入格式：

输入文件的第 1 行包含 2 个整数，依次为n, m，表示 drd 有n扇防御门，atm 的初始攻击力为0到m之间的整数。

接下来n行，依次表示每一扇防御门。每行包括一个字符串op和一个非负整数t，两者由一个空格隔开，且op在前，t在后，op表示该防御门所对应的操作，t表示对应的参数。

输出格式：

输出一行一个整数，表示atm的一次攻击最多使drd受到多少伤害。

说明：

---

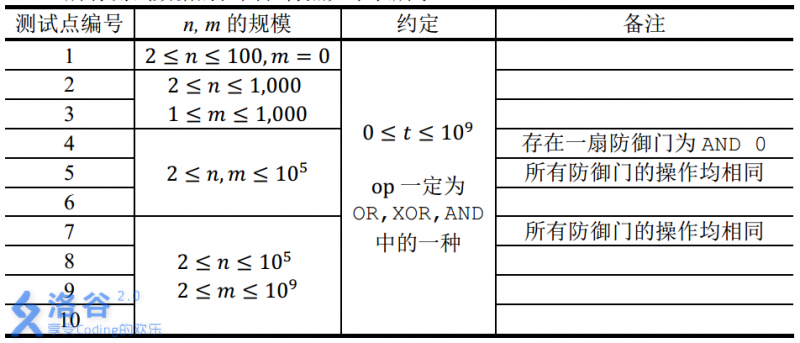
发现每一位是独立的，我们可以花\(nlogm\)的时间把每一位填0或1的情况的结果存下来

然后似乎可以贪心，我不太清楚

我是对每一位做的DP，用来判断某位是否可以越界

---

Code:

#include <cstdio>
const int N=1e5+10;
struct node
{
    int op,t;
}opt[N];
int n,m,to[32][2],dp[32][2];//0表示有限制，1表示没有
int max(int x,int y){return x>y?x:y;}
int main()
{
    scanf("%d%d",&n,&m);
    char op[6];
    for(int i=1;i<=n;i++)
    {
        scanf("%s%d",op,&opt[i].t);
        if(op[0]=='A') opt[i].op=1;
        else if(op[0]=='O') opt[i].op=2;
        else opt[i].op=3;
    }
    for(int k=0;k<30;k++)
    {
        for(int s=0;s<=1;s++)
        {
            to[k][s]=s;
            for(int i=1;i<=n;i++)
            {
                int op=opt[i].op,t=opt[i].t;
                if(op==1) to[k][s]&=t>>k&1;
                else if(op==2) to[k][s]|=t>>k&1;
                else to[k][s]^=t>>k&1;
            }
        }
    }
    int cnt=0,sum=0,ans=0;
    for(int p=m;p;p>>=1) ++cnt;
    for(int k=0;k<30;k++)
    {
        if(k>=cnt)
            sum|=to[k][0]<<k;
        else
        {
            if(cnt>k)//不处理最后一位
                dp[k][1]=dp[k-1][1]|((to[k][0]|to[k][1])<<k);//最大化
            dp[k][0]=dp[k-1][0]|((to[k][0])<<k);//填0不能随便用
            if(m>>k&1)//如果这一位可以填1
            {
                dp[k][0]=max(dp[k][0],dp[k-1][0]|(to[k][1]<<k));//填1不能随便用
                dp[k][0]=max(dp[k][0],dp[k-1][1]|(to[k][0]<<k));//填0前面随便用
            }
            ans=max(ans,max(dp[k][0],dp[k][1]));
        }
    }
    printf("%d\n",ans+sum);
    return 0;
}

---

2018.9.3