Codeforces Round #460 (Div. 2).E 费马小定理+中国剩余定理

E. Congruence Equation

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Given an integer x. Your task is to find out how many positive integers n (1 ≤ n ≤ x) satisfy

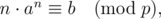where a, b, p are all known constants.

Input

The only line contains four integers a, b, p, x (2 ≤ p ≤ 106 + 3, 1 ≤ a, b < p, 1 ≤ x ≤ 1012). It is guaranteed that p is a prime.

Output

Print a single integer: the number of possible answers n.

Examples

input

2 3 5 8

output

2

input

4 6 7 13

output

1

input

233 233 10007 1

output

1

Note

In the first sample, we can see that n = 2 and n = 8 are possible answers.

题意：给出a, b, p, x，求有多少个n满足:n*a^n%p==b(n<=x)

思路：先要知道一个很简单的性质：a^n%p=(a%p)^(n%p-1)%p=a^(n%p-1),即a^n仅有p-1种结果。

①暴力枚举a^i%p (i从0到p-1)算出每个余数，可以得到式子n*a^i%p==b

②对于每个a^i，用逆元求出c，n%p = c= b*inv(a^i)%p

③则n%(p-1)==i 且n%p==c，最小的n可以用CRT求出，n的周期是P=p*(p-1).

代码：

 //#include "bits/stdc++.h"
 #include "cstdio"
 #include "map"
 #include "set"
 #include "cmath"
 #include "queue"
 #include "vector"
 #include "string"
 #include "cstring"
 #include "time.h"
 #include "iostream"
 #include "stdlib.h"
 #include "algorithm"
 #define db double
 #define ll long long
 //#define vec vector<ll>
 #define Mt  vector<vec>
 #define ci(x) scanf("%d",&x)
 #define cd(x) scanf("%lf",&x)
 #define cl(x) scanf("%lld",&x)
 #define pi(x) printf("%d\n",x)
 #define pd(x) printf("%f\n",x)
 #define pl(x) printf("%lld\n",x)
 #define inf 0x3f3f3f3f
 #define rep(i, x, y) for(int i=x;i<=y;i++)
 const int N   = 1e6 + ;
 const int mod = 1e9 + ;
 const int MOD = mod - ;
 const db  eps = 1e-;
 const db  PI  = acos(-1.0);
 using namespace std;
 ll a,b,p,x;
 ll m[],f[];
 ll exgcd(ll a, ll b, ll &x, ll &y)
 {
     ll d;
     //if (a == 0 && b == 0) return -1;
     if (b == )
     {
         x = ;
         y = ;
         return a;
     }
     d = exgcd(b, a%b, y, x);
     y -= a / b * x;
     return d;
 }

 ll inv(ll a, ll MOD)
 {
     ll x, y, d;
     d = exgcd(a, MOD, x, y);
     if (d == )
         return (x % MOD + MOD) % MOD;
     // else   return -1;
 }
 ll china(ll *f, ll *m){
     ll M = , ret = ;
     for(int i = ; i < ; i ++) M *= m[i];
     for(int i = ; i < ; i ++){
         ll w = M / m[i];
         ret = (ret + w * inv(w, m[i]) * f[i]) % M;
     }
     return (ret + M) % M;
 }
 ll qpow(ll x,ll n)
 {
     ll ans=;
     x%=p;
     while(n){
         if(n&) ans=ans*x%p;
         x=x*x%p;
         n>>=;
     }
     return  ans;
 }

 int main()
 {
     cl(a),cl(b),cl(p),cl(x);
     a%=p;
     ll ans=,P=p*(p-);
     m[]=p-,m[]=p;
     for(int i=;i<p-;i++)
     {
         f[]=i;
         f[]=inv(qpow(a,i),p)*b%p;
         ll xx=china(f,m);
         ans+=(x-xx+P)/P;
     }
     pl(ans);
     return ;
 }