梯度下降&随机梯度下降&批梯度下降

梯度下降法

​ 下面的h(x)是要拟合的函数，J(θ)损失函数，theta是参数，要迭代求解的值，theta求解出来了那最终要拟合的函数h(θ)就出来了。其中m是训练集的记录条数，j是参数的个数。

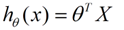
梯度下降法流程：

（1）先对θ随机赋值，可以是一个全零的向量。

（2）改变θ的值，使J(θ)按梯度下降的方向减少。

以上式为例：

（1）对于我们的函数J(θ)求关于θ的偏导：

（2）下面是更新的过程，也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值，-后面的部分表示按梯度方向减少的量，α表示步长，也就是每次按照梯度减少的方向变化多少。

值得注意的是，梯度是有方向的，对于一个向量θ，每一维分量θi都可以求出一个梯度的方向，我们就可以找到一个整体的方向，在变化的时候，我们就朝着下降最多的方向进行变化就可以达到一个最小点，不管它是局部的还是全局的。

批量梯度下降

​ （1）将J(θ)对θ求偏导，得到每个θ对应的梯度（m为训练样本的个数）：

​ （2）由于是要最小化风险函数，所以按每个参数theta的梯度负方向，来更新每个theta

​ （3）从上面公式可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集所有的数据，如果m很大，那么可想而知这种方法的迭代速度！！所以，这就引入了另外一种方法，随机梯度下降。

随机梯度下降

​ （1）上面的风险函数可以写成如下这种形式，损失函数对应的是训练集中每个样本的粒度，而上面批量梯度下降对应的是所有的训练样本：

（2）每个样本的损失函数，对theta求偏导得到对应梯度，来更新theta

（3）随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。