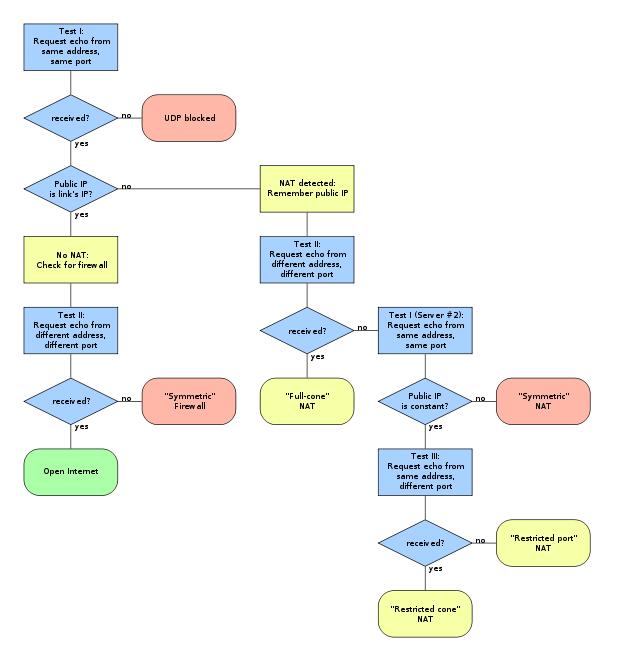
Stun方式的P2P实现原理(转)
Stun方式的P2P实现原理(转)的更多相关文章
- P2P的原理和常见的实现方式(为libjingle开路)
参考原文 为了项目的IM应用,最近在研究libjingle,中间看了也收集了很多资料,感慨网上很多资料要么太过于纠结协议(如STUN.ICE等)实现细节,要么中间有很多纰漏.最后去伪存真,归纳总结了一 ...
- P2P的原理和常见的实现方式
参考资料:http://www.cppblog.com/peakflys/archive/2013/01/25/197562.html P2P实现的原理 首先先介绍一些基本概念: NAT(Net ...
- 转载:P2P技术原理及应用(1)
转帖allen303allen的空间 作 者:金海 廖小飞 摘要:对等网络(P2P)有3种主要的组织结构:分布式哈希表(DHT)结构.树形结构.网状结构.P2P技术已 经延伸到几乎所有的网络应用领域, ...
- 穿透内网,连接动态ip,内网ip打洞-----p2p实现原理(转)
源: 穿透内网,连接动态ip,内网ip打洞-----p2p实现原理
- P2P通讯原理
1.简介 当今互联网到处存在着一些中间件(MIddleBoxes),如NAT和防火墙,导致两个(不在同一内网)中的客户端无法直接通信.这些问题即便是到了IPV6时代也会存在,因为即使不需要NAT,但还 ...
- P2P通信原理与实现(C++)
1.简介 当今互联网到处存在着一些中间件(MIddleBoxes),如NAT和防火墙,导致两个(不在同一内网)中的客户端无法直接通信.这些问题即便是到了IPV6时代也会存在,因为即使不需要NAT,但还 ...
- p2p通信原理及实现(转)
1.简介 当今互联网到处存在着一些中间件(MIddleBoxes),如NAT和防火墙,导致两个(不在同一内网)中的客户端无法直接通信.这些问题即便是到了IPV6时代也会存在,因为即使不需要NAT,但还 ...
- 浅谈P2P终结者原理及其突破
P2P终结者按正常来说是个很好的网管软件,但是好多人却拿它来,恶意的限制他人的流量,使他人不能正常上网,下面我们就他的功能以及原理还有突破方法做个详细的介绍! 我们先来看看来自在网上PSP的资料:P2 ...
- 内网ip打洞-----p2p实现原理
网上找了非常多.代码大堆,原理讲清楚透彻的不多. 本人找几篇讲得好的来整理一下. 一片技术文章,最基本的讲清楚原理.假设再有完整的能执行的源码也可,关键是要把核心部分代码分析清楚. (1)问题的由来: ...
随机推荐
- ie 元素兼容性总结
css 属性元素 2.z-index 正常按自身层级决定显示顺序,在ie6 7 还需要依赖于父级的层级决定,排布在后边的元素排在前面.后来者居上覆盖前者. IE6,7支持inline元素转换成inli ...
- gbk编码汉字转换成对应的十进制十六进制的值
http://www.mytju.com/classcode/tools/urlencode_gb2312.asp
- 26 python 并发编程之多进程理论
一 什么是进程 进程:正在进行的一个过程或者说一个任务.而负责执行任务则是cpu. 举例(单核+多道,实现多个进程的并发执行): egon在一个时间段内有很多任务要做:python备课的任务,写书的任 ...
- Spring_总结_04_高级配置(三)_处理歧义
一.前言 本文承接上一节:Spring_总结_04_高级配置(二)之条件注解@Conditional 我们前面装配bean时,在Spring容器中,都是只有一个bean能匹配所需的结果. 如果有多个b ...
- Spring与RMI集成实现远程访问
使用spring对RMI的支持,可以非常容易地构建你的分布式应用.在服务端,可以通过Spring的org.springframework.remoting.rmi.RmiServiceExporter ...
- 字符集、字符编码、XML中的中文编码
字符集.字符编码.XML中的中文编码 作为程序员的你是不是对于ASCII .UNICODE.GB2321.UTF-7.UTF-8等等不时出现在你面前的这些有着奇怪意义的词感到很讨厌呢,是不是总觉得好象 ...
- js改变select的选中项不触发select的change事件
// test var selectEl = document.querySelector('select') var buttonEl = document.querySelector('butto ...
- [基本操作] Mobius 反演, Dirichlet 卷积和杜教筛
Dirichlet 卷积是两个定义域在正整数上的函数的如下运算,符号为 $*$ $(f * g)(n) = \sum_{d|n}f(d)g(\frac{n}{d})$ 如果不强调 $n$ 可简写为 $ ...
- POJ - 3150 :Cellular Automaton(特殊的矩阵,降维优化)
A cellular automaton is a collection of cells on a grid of specified shape that evolves through a nu ...
- 转载:maven依赖范围
其中依赖范围scope 用来控制依赖和编译,测试,运行的classpath(注意是与classpath)的关系. 主要的是三种依赖关系如下:1.compile: 默认编译依赖范围.对于编译,测试,运行 ...
