poj 1390 区间dp

Blocks

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 5035		Accepted: 2065

Description

Some of you may have played a game called 'Blocks'. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold. 
The corresponding picture will be as shown below: 
 
Figure 1
If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.

Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points.

Now let's look at the picture below: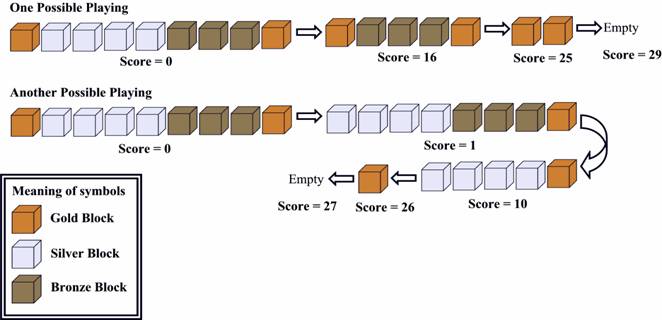 
 
Figure 2

The first one is OPTIMAL.

Find the highest score you can get, given an initial state of this game.

Input

The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range 1~n.

Output

For each test case, print the case number and the highest possible score.

Sample Input

2
9
1 2 2 2 2 3 3 3 1
1
1

Sample Output

Case 1: 29
Case 2: 1

Source

Liu Rujia@POJ

 

题意：N个方盒(box)摆成一排，每个方盒有自己的颜色。连续摆放的同颜色方盒构成 一个方盒片段(box segment)玩家每次点击一个方盒，则该方盒所在方盒片段就会消失。若消失的方盒片段 中共有k个方盒，则玩家获得k*k个积分 求获得的最高积分

 

题解：参考pku_gw代码   dp姿势涨

score[i][j][len] 表示在i~j的方盒片段上 片段j右侧有长度为len的且与j颜色相同的片段 获得的最高分

但是左侧的和j颜色相同的怎么处理呢  就需要枚举左侧的片段，判断分块处理j片段更优还是合并处理

更优  递归的终止条件问i==j

 

 /******************************
 code by drizzle
 blog: www.cnblogs.com/hsd-/
 ^ ^    ^ ^
  O      O
 ******************************/
 //#include<bits/stdc++.h>
 #include<iostream>
 #include<cstring>
 #include<cmath>
 #include<cstdio>
 #define ll long long
 #define mod 1000000007
 #define PI acos(-1.0)
 using namespace std;
 int t;
 int n;
 struct node
 {
     int color;
     int len;
 }se[];
 int score[][][];
 int fun(int l,int r,int len)
 {
  if(score[l][r][len]>)
         return score[l][r][len];
  int re=(se[r].len+len);//直接处理右侧
  re=re*re;
  if(l==r)
  {
      score[l][r][len]=re;
      return score[l][r][len];
  }
  re+=fun(l,r-,);
  for(int j=r-;j>=l;j--)//枚举左侧片段
  {
      if(se[j].color!=se[r].color) continue;
      int temp=fun(l,j,se[r].len+len)+fun(j+,r-,);//递归 分解 将右侧的合并到左侧
      if(temp<=re) continue;//判断那个更优
      re=temp;
      break;
  }
  score[l][r][len]=re;
  return score[l][r][len];
 }
 int main()
 {
     scanf("%d",&t);
     int coun=;
     int flag=;
     memset(se,,sizeof(se));
     while(t--){
         int coun=;
         int exm;
         scanf("%d",&n);
         scanf("%d",&se[coun].color);
         se[coun].len=;
         for(int i=;i<n;i++)//分解片段的过程
         {
             scanf("%d",&exm);
             if(exm==se[coun].color)
                 se[coun].len++;
             else
             {
                 coun++;
                 se[coun].color=exm;
                 se[coun].len=;
             }
         }
         memset(score,,sizeof(score));
         printf("Case %d: %d\n",flag++,fun(,coun,));
     }
     return ;
 }