Intersection（poj）

Intersection

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 13140		Accepted: 3424

Description

You are to write a program that has to decide whether a given line segment intersects a given rectangle.

An example:

line: start point: (4,9)

end point: (11,2)

rectangle: left-top: (1,5)

right-bottom: (7,1)

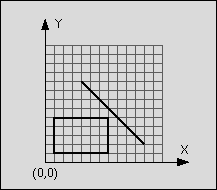
Figure 1: Line segment does not intersect rectangle

The line is said to intersect the rectangle if the line and the
rectangle have at least one point in common. The rectangle consists of
four straight lines and the area in between. Although all input values
are integer numbers, valid intersection points do not have to lay on the
integer grid.

Input

The
input consists of n test cases. The first line of the input file
contains the number n. Each following line contains one test case of the
format:

xstart ystart xend yend xleft ytop xright ybottom

where (xstart, ystart) is the start and (xend, yend) the end point
of the line and (xleft, ytop) the top left and (xright, ybottom) the
bottom right corner of the rectangle. The eight numbers are separated by
a blank. The terms top left and bottom right do not imply any ordering
of coordinates.

Output

For
each test case in the input file, the output file should contain a line
consisting either of the letter "T" if the line segment intersects the
rectangle or the letter "F" if the line segment does not intersect the
rectangle.

Sample Input

1
4 9 11 2 1 5 7 1

Sample Output

F
题解：判断直线与矩形是否有公共点：a=y2-y1;b=x1-x2;c=x2*y1-x1*y2;
代码：

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<cstring>
 using namespace std;
 const int INF=0x3f3f3f3f;
 const double PI=acos(-1.0);
 typedef long long LL;
 struct Node{
     int x,y;
 }s,e,a,d;
 int m,n,q;
 int count(int x,int y){
     return m*x+n*y+q;
 }
 int main(){
     int T;
     scanf("%d",&T);
     while(T--){
         scanf("%d%d%d%d%d%d%d%d",&s.x,&s.y,&e.x,&e.y,&a.x,&a.y,&d.x,&d.y);
         if(a.x>d.x){
             int temp=a.x;
             a.x=d.x;
             d.x=temp;
         }
         if(a.y<d.y){
             int temp=a.y;
             a.y=d.y;
             d.y=temp;
         }
         m=e.y-s.y;
         n=s.x-e.x;
         q=e.x*s.y-s.x*e.y;
         if(count(a.x,a.y)*count(d.x,d.y)>&&count(a.x,d.y)*count(d.x,a.y)>){
             puts("F");continue;
         }
         if((s.x<a.x&&e.x<a.x)||(s.x>d.x&&e.x>d.x)||(s.y>a.y&&e.y>a.y)||(s.y<d.y&&e.y<d.y))//检查是否包含
             puts("F");
         else puts("T");
     }
     return ;
 }