【初识——最大流】 hdu 1532 Drainage Ditches（最大流） USACO 93

最大流首次体验感受——

什么是最大流呢？

从一个出发点（源点），走到一个目标点（汇点），途中可以经过若干条路，每条路有一个权值，表示这条路可以通过的最大流量。

最大流就是从源点到汇点，可以通过的最大流量。

接下来我们看一个图——

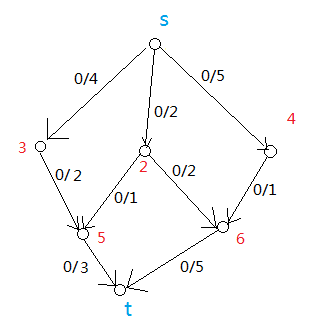图1

这个图中，s是源点，t是汇点。期间可以经过2, 3, 4, 5, 6几个点。每条边上有两个权值，其中第一个表示当前通过这条边的流量，第二个表示这条边最大可以通过的流量。

最佳情况，即最大可以通过的流量的一种情况是这样的——

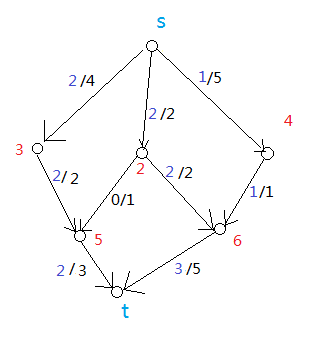图2

但还有一种情况，同样可以达到最大流——

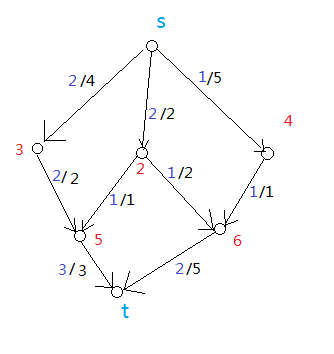图3

这里得到两个结论：

1. 每条路径中都有至少一条边是满的。

2. 最大流可能不止一种情况。

接下来我们再看另一个图：

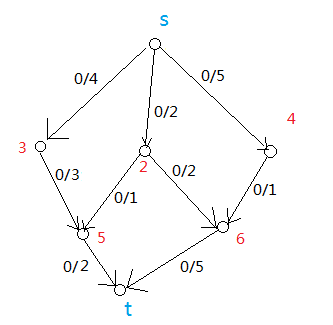图4

如果在这个图上找最大流该怎么找？

这样？

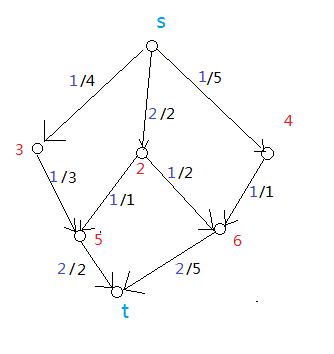图5

不对，这个图乍一看好像满足每条路径上都有一个满流的边这个条件，但是其实还有更大的流——

图6

怎么办呢？

我们可以通过这个方式从图5变到图6——

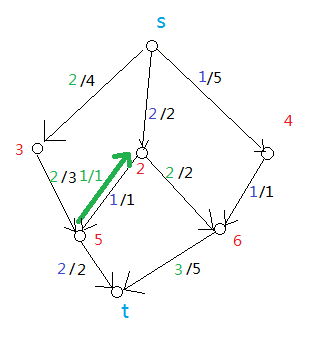图7

这里我们的可以这样理解，在我们走出图5 的结果以后，我们允许图中出现图7中的绿色的边，然后我们就得到了绿色的数字所标示出的一条新路，通过这条路径，我们就获得了最大流。

如果我们获得了一个流量图，这个流量图中每条路径上都有一条边是满流了，如何判断这是不是一个最大流的图呢？通过上面的方法，我们在通过某条边之后，在这两个点之间构造一条反向的并且和通过的流量大小相同的边（称为反向边）。这样，就可能产生一条新路，使整个图中的流量增加。那么，我们不断地构造这种边，直到无法寻找到新的路径为止（称为增广路径），是不是就得到了最大流呢？

总结起来，每次找到一条增广路，增广路中每条边的值，都减去路径中，边值最小的边的值（读起来很凹口是不是？多读几遍就好了）。同时，还要给每条边都加上反向边。重复寻找，直到找不到新的路径，我们就获得了这个图的最大流。

注意，

1. 每次寻找增广路径后，我们都会将原图更改，这样，我们会得到一个新的图。
2. 在获得最大流的图之前，我们获得的每张图都称为残余网络。原始图也可以视为残余网络。

以上讲的是寻找最大流的思想。

但是，寻找增广路径的方法不止一种。

我最直接想到的方法，使用dfs多次搜索这张图，直到找不到为止。

 #include <cstdio>
 #include <cmath>
 #include <cstring>
 #include <algorithm>
 using namespace std;

 const int N = ;
 const int M = ;

 int n, m;
 int mp[N][N];               //保存地图信息，有向图
 bool vis[N][N];             //dfs时标记使用
 int ans;                    //最终结果

 void init()
 {
     memset(mp, , sizeof(mp));
     memset(vis, , sizeof(vis));
     for(int i = ; i < n; i++)
     {
         int a, b, c;
         scanf("%d%d%d", &a, &b, &c);
         mp[a][b] += c;
     }
     ans = ;
 }

 int dfs(int x, int maxn)
 {
     if(x == m)
     {
         ans += maxn;        //每次走到汇点后增加的流量
         return maxn;
     }
     int flow = ;
     for(int i = ; i <= m; i++)
     {
         if(mp[x][i] >  && !vis[x][i])
         {
             vis[x][i] = ;
             int mmaxn = maxn < mp[x][i] ? maxn : mp[x][i];      //取本路径中所可以通过的最小值
             int mid;
             if(mmaxn > ) mid = dfs(i, mmaxn);                  //如果此路仍然是通路，则继续搜索
             if(mid > )
             {
                 mp[x][i] -= mid;                        //已经经过的路要减去耗费的流量
                 mp[i][x] += mid;                        //反向路（弧）增加耗费的流量
                 maxn -= mid;                            //走过一条通路后剩余的流量
                 flow += mid;                            //已经消耗的流量
                 if(maxn == ) break;
             }
         }
     }
     return flow;
 }

 int main()
 {
     //freopen("test.in", "r", stdin);
     while(~scanf("%d%d", &n, &m))
     {
         init();
         while(dfs(, M) > ) memset(vis, , sizeof(vis));
         printf("%d\n", ans);
     }
     return ;
 }

dfs

但是后来我突然想到。dfs找到的不一定最短路，每次搜索可能会浪费时间，然后又改成了bfs，这种方法也就是常说的Edmonds-Karp算法。

 #include <cstdio>
 #include <cmath>
 #include <cstring>
 #include <algorithm>
 #include <queue>
 using namespace std;

 const int N = ;
 const int M = ;

 int mp[N][N];
 int fm[N];              //用于记录路径
 int val[N];
 int n, m;
 int ans;

 void init()
 {
     memset(mp, , sizeof(mp));
     for(int i = ; i < n; i++)
     {
         int a, b, c;
         scanf("%d%d%d", &a, &b, &c);
         mp[a][b] += c;
     }
     ans = ;
 }

 void work()
 {
     while()
     {
         memset(val, , sizeof(val));
         val[] = M;
         queue<int> que;
         que.push();
         while(!que.empty())             //spfa，寻找最短路
         {
             int k = que.front();
             que.pop();
             if(k == m) break;
             for(int i = ; i <= m; i++)
             {
                 if(!val[i] && mp[k][i] > )
                 {
                     fm[i] = k;
                     que.push(i);
                     val[i] = val[k] < mp[k][i] ? val[k] : mp[k][i];
                 }
             }
         }
         if(val[m] == ) break;                  //当前图上找不到源点到汇点的通路，则退出

         for(int i = m; i != ; i = fm[i])
         {
             mp[fm[i]][i] -= val[m];             //经过的路径上要减去耗费的流量
             mp[i][fm[i]] += val[m];             //反向路径（弧）增加相应的路径
         }
         //printf("%5d\n", val[m]);
         ans += val[m];                          //结果增加新增的流量
     }
 }

 void outit()
 {
     printf("%d\n", ans);
 }

 int main()
 {
     while(~scanf("%d%d", &n, &m))
     {
         init();
         work();
         outit();
     }
     return ;
 }

bfs

接下来又找到了一种看起来很高大上的方法——Dinic算法。

这个方法要说一说，因为我也花了不少时间来理解，虽然还没有完全理解，但是已经被它所包含的思想震撼了。

这个算法是一层一层搜索的。简单来说，就是：

1）将这个图中用bfs遍历一遍，严格确立每个点的层次。

如果使用bfs可以从源点走到汇点，那么执行2），否则这张图中不存在新的增广路，算法结束。

2）从源点开始dfs，寻找到当前图中所有从源点到汇点的路径，在寻找时，严格按照点的层次寻找，只能从第i层的点走到第i+1层的点。

3）重复1）。

好神奇的方法。

 #include <cstdio>
 #include <cmath>
 #include <cstring>
 #include <algorithm>
 #include <queue>
 using namespace std;

 const int N = ;
 const int M = ;

 int mp[N][N];
 int dis[N];
 int cur[N];
 bool vis[N];
 int n, m;
 int ans;

 void init()
 {
     memset(mp, , sizeof(mp));
     for(int i = ; i < n; i++)
     {
         int a, b, c;
         scanf("%d%d%d", &a, &b, &c);
         mp[a][b] += c;
     }
     ans = ;
 }

 bool bfs()
 {
     memset(vis, , sizeof(vis));
     queue<int> que;
     que.push();
     dis[] = ;
     vis[] = ;
     while(!que.empty())
     {
         int k = que.front();
         que.pop();
         for(int i = ; i <= m; i++)
         {
             if(!vis[i] && mp[k][i] > )
             {
                 vis[i] = ;
                 dis[i] = dis[k]+;
                 que.push(i);
             }
         }
     }
     return vis[m];
 }

 int dfs(int x, int val)
 {
     if(x == m) return val;
     int flow = , minn;
     for(int& i = cur[x]; i <= m; i++)       //随着i的变化改变cur[x],这样可以节省当前图中下次使用x时耗费的时间
     {
         int mval = val < mp[x][i] ? val : mp[x][i];     //记录当前路径中的最小的边的权，最后要根据它建立反向边
         if(dis[x]+ == dis[i])
         {
             minn = ;
             if(mval > ) minn = dfs(i, mval);
             if(minn > )
             {
                 mp[x][i] -= minn;
                 mp[i][x] += minn;
                 flow += minn;
                 val -= minn;
                 if(val == ) break;
             }
         }

     }
     return flow;
 }

 void work()
 {
     while(bfs())        //如果存在增广路，则dfs寻找，否则结束
     {
         for(int i = ; i <= m; i++) cur[i] = ;
         ans += dfs(, M);
     }
 }

 void outit()
 {
     printf("%d\n", ans);
 }

 int main()
 {
     //freopen("test.in", "r", stdin);
     while(~scanf("%d%d", &n, &m))
     {
         init();
         work();
         outit();
     }
     return ;
 }

Dinic