斐波那契(Fibonacci)数列的几种计算机解法

　　题目：斐波那契数列，又称黄金分割数列（F(n+1)/F(n)的极限是1:1.618，即黄金分割率），指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……。在数学上，斐波纳契数列以如下被以递归的方法定义：

　　　　　　　　　　　　　　F(0)=0，F(1)=1，F(n)=F(n-1)+F(n-2)（n≥2，n∈N*）

　　递归实现——自上而下

　　

　　在很多C语言教科书中讲到递归函数的时候，都会用Fibonacci作为例子。因此很多程序员对这道题的递归解法非常熟悉，看到题目就能写出如下递归求解的代码：

long Fibonacci(long n)                          //递归算法
{
    if(n<=)    return n;                       //终止递归的条件
    else return Fibonacci(n-) + Fibonacci(n-);//递归步骤
}

　　

　　但是，教科书上反复用这个题目来讲解递归函数，并不能说明递归解法最适合这道题目。我们以求解F(10)作为例子来分析递归求解的过程。要求得F(10)，需要求得F(9)和F(8)。同样，要求得F(9)，要先求得F(8)和F(7)……我们用下面的树形结构来表示这种依赖关系

　　　　　　 　　F(10)
               　　　　　　　   /             \
           　　　　　　　　 F(9)          F(8)
         　　　　　　　　  /     \           /    \
      　　　　　　　　 F(8)    F(7)   F(7)   F(6)
     　　　　　　　　 /    \      /    \ 
   　　　　　　　 F(7)  F(6) F(6)  F(5)

　　我们不难发现在这棵树中有很多结点会重复的，而且重复的结点数会随着n的增大而急剧增加。这意味这计算量会随着n的增大而急剧增大。例如，在递归计算F(10)时，F(3)的值被计算了21次。而在递归计算F(30)，这个调用的次数是骇人的317811次！这些个计算实际上只有一次是必要的，其余的纯属浪费！

　　事实上这个递归算法的时间复杂度是指数级Ω(φⁿ)，φ=1.618（1:1.618=0.618称为黄金分割率）。

　　迭代算法——自底向上

　　下面的程序使用一个简单循环迭代来代替递归，这个非递归的形式不如上文给出的递归简单，也不太符合Fibonacci的递归定义，但是，它的运行速度提高了特别多！

　　迭代算法的源码如下：

// 计算斐波那契数列的非递归算法(迭代)
long Fibonacci(long n)
{
    if(n<=)    return n;                                // Fib(0)或Fib(1)的情况
    long FibCurrent, FibTwoBack = , FibOneBack = ;     // 用数组保存程序更简洁，但不能明显的看出迭代的思想
    for(int i= ; i<=n ; i++)                            // n≥2的情况
    {
        FibCurrent = FibOneBack + FibTwoBack;            // 计算Fib(i)=Fib(i-1)+Fib(i-2)
        /* 下面的保存顺序不能对调 */
        FibTwoBack = FibOneBack;                         // 保存Fib(i-1)作为下趟的Fib(i-2)
        FibOneBack = FibCurrent;                         // 保存Fib(i)作为下趟的Fib(i-1)

    }
    return FibCurrent;
}

　　显然，这个算法的时间复杂度为O(n)，相比于前面指数级的递归算法，有了质的飞跃。

　　事实上，这还不是最快的算法。还有一种时间复杂度是O(logn)的方法

　　转化为特征矩阵乘方——分治策略 + 矩阵快速幂

　　由数学归纳法易证：

　　　　　　　　　　

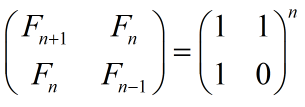
　　问题转化为求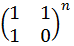，继而就求出了F(n)。

　　对于乘方问题我们利用分治策略优化有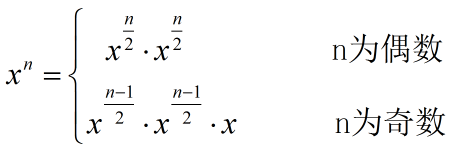 

　　运行时间递归式：T(n) = T(n/2) + θ(1) （同二分搜索一样）　   用主方法接得T(n) = θ(logn)

　　利用对特征矩阵乘方优化的方法可以得到最小的运行时间复杂度O(logn)，代码如下：

class Matrix    // 自定义2×2矩阵类
{
public:
    unsigned int a11, a12, a21, a22;    // 矩阵元素
    Matrix(int a, int b, int c, int d) :a11(a), a12(b), a21(c), a22(d) {}// 构造函数
    Matrix operator*(const Matrix &other)    // 重载矩阵的乘法
    {
        Matrix result(, , , );
        result.a11 = a11*other.a11 + a12*other.a21;
        result.a12 = a11*other.a12 + a12*other.a22;
        result.a21 = a21*other.a11 + a22*other.a21;
        result.a22 = a21*other.a12 + a22*other.a22;
        return result;
    }
};

Matrix MatrixPow(const Matrix &A, unsigned int n)// 计算矩阵A的n次方(分治策略,此处自底向上迭代)
{
    Matrix result(, , , );    // 单位矩阵
    Matrix tmp = A;
    while (n)
    {
        if (n & )                // &为按位"与"运算,如果n为奇数
            result = result * tmp;// 单乘一次矩阵
        tmp = tmp * tmp;
        n = n >> ;               // n右移一位,相当于n/2(向下取整)
    }
    return result;
}

unsigned int Fibonacci(int n)
{
    if (n <= )
        return n;
    Matrix A(, , , );               // 特征矩阵
    Matrix result = MatrixPow(A, n);    // 计算矩阵A的n次方
    return result.a12;                  // Fn即为结果矩阵中第一行第二例上的元素
}

　　　　参考资料：　《MIT算法导论公开课》第三集——分治法

　　　　　　　　　　《编程之美》P163

　　　　　　　　　　《剑指offer》P73