格点拉格朗日插值与PME算法

技术背景

在前面的一篇博客中，我们介绍了拉格朗日插值法的基本由来和表示形式。这里我们要介绍一种拉格朗日插值法的应用场景：格点拉格朗日插值法。这种场景的优势在于，如果我们要对整个实数空间进行求和或者积分，计算量是随着变量的形状增长的。例如分子动力学模拟中计算静电势能，光是计算电荷分布函数都是一个\(O(N^2)\)的计算量，其中\(N\)表示点电荷数量。而如果我们对空间进行离散化，划分成一系列的格点，再对邻近的常数个格点进行插值，那么我们的求和计算量可以缩减到\(O(N)\)。

格点拉格朗日插值

给定一个函数\(y=f(x-x_r)\)，我们可以将其插值到最近的4个整数格点上：\(\lfloor x_r\rfloor-1.5,\lfloor x_r\rfloor-0.5,\lfloor x_r\rfloor+0.5,\lfloor x_r\rfloor+1.5\)，根据拉格朗日插值形式有：

\[y_{interp}=c_1(x)f(\lfloor x_r\rfloor-1.5-x_r)+c_2(x)f(\lfloor x_r\rfloor-0.5-x_r)+c_3(x)f(\lfloor x_r\rfloor+0.5-x_r)+c_4(x)f(\lfloor x_r\rfloor+1.5-x_r)
\]

如果以\(\lfloor x_r\rfloor\)最近的中心点为原点，即\(\lfloor x_r\rfloor=0\)，则其系数有：

\[\begin{align*}
c_1(x)&=\frac{(x-\lfloor x_r\rfloor+0.5)(x-\lfloor x_r\rfloor-0.5)(x-\lfloor x_r\rfloor-1.5)}{-6}=\frac{1}{48}(-8x^3+12x^2+2x-3)\\
c_2(x)&=\frac{(x-\lfloor x_r\rfloor+1.5)(x-\lfloor x_r\rfloor-0.5)(x-\lfloor x_r\rfloor-1.5)}{2}=\frac{1}{16}(8x^3-4x^2-18x+9)\\
c_3(x)&=\frac{(x-\lfloor x_r\rfloor+1.5)(x-\lfloor x_r\rfloor+0.5)(x-\lfloor x_r\rfloor-1.5)}{-2}=\frac{1}{16}(-8x^3-4x^2+18x+9)\\
c_4(x)&=\frac{(x-\lfloor x_r\rfloor+1.5)(x-\lfloor x_r\rfloor+0.5)(x-\lfloor x_r\rfloor-0.5)}{6}=\frac{1}{48}(8x^3+12x^2-2x-3)
\end{align*}
\]

其图像大致如下图所示（图片来自于参考链接1）：

对于多维的格点拉格朗日插值，则是一个叉乘的关系，其图像为：

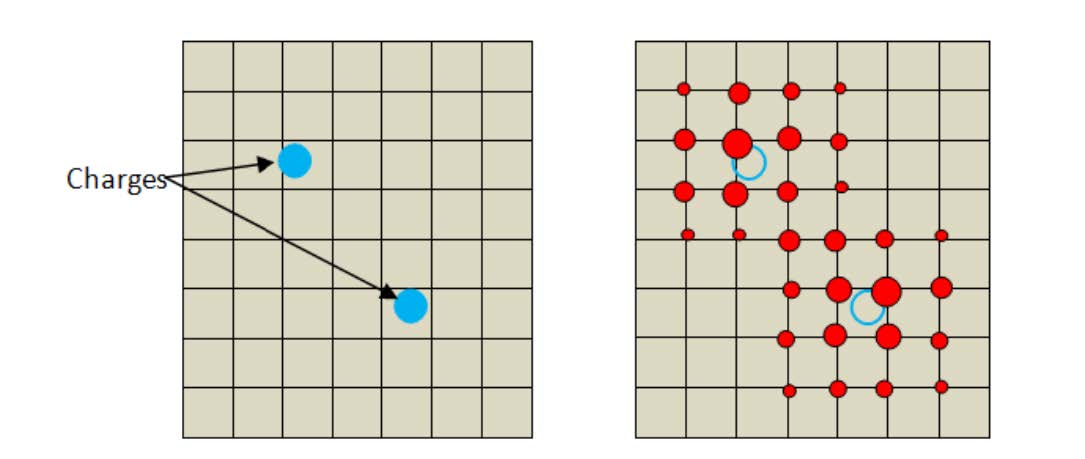
PME算法

我们把上面得到的这个格点拉格朗日插值应用到静电势能的计算中。在前面一篇博客介绍的静电势计算中，有一项电荷分布函数是这样的：

\[s(\mathbf{k})=|S(\mathbf{k})|^2=\sum_{i=0}^{N-1}q_ie^{-j\mathbf{k}\mathbf{r}_i}\sum_{l=0}^{N-1}q_le^{j\mathbf{k}\mathbf{r}_l}
\]

其中\(S(\mathbf{k})=\sum_{i=0}^{N-1}q_ie^{j\mathbf{k}\mathbf{r}_i}=\sum_{i=0}^{N-1}q_ie^{j\mathbf{k}_xx_i}e^{j\mathbf{k}_yy_i}e^{j\mathbf{k}_zz_i}\)。把后面这几个指数项用格点拉格朗日插值替代得：

\[S(\mathbf{k})=\sum_{i=0}^{N-1}q_i\sum_{x,y,z}\left[c_1(x)f(\lfloor x_i\rfloor-1.5-x_i)+c_2(x)f(\lfloor x_i\rfloor-0.5-x_i)+c_3(x)f(\lfloor x_i\rfloor+0.5-x_i)+c_4(x)f(\lfloor x_i\rfloor+1.5-x_i)\right]\left[c_1(y)f(\lfloor y_i\rfloor-1.5-y_i)+c_2(y)f(\lfloor y_i\rfloor-0.5-y_i)+c_3(y)f(\lfloor y_i\rfloor+0.5-y_i)+c_4(y)f(\lfloor y_i\rfloor+1.5-y_i)\right]\left[c_1(z)f(\lfloor z_i\rfloor-1.5-z_i)+c_2(z)f(\lfloor z_i\rfloor-0.5-z_i)+c_3(z)f(\lfloor z_i\rfloor+0.5-z_i)+c_4(z)f(\lfloor z_i\rfloor+1.5-z_i)\right]
\]

有了函数形式以后，我们可以简写\(S(\mathbf{k})\)为一个关于三维空间格点的求和：

\[S(\mathbf{k})=\sum_{i=0}^{N-1}q_i\sum_{m_x=\lfloor x_{min}\rfloor-1.5}^{\lfloor x_{max}\rfloor+1.5}\sum_{m_y=\lfloor y_{min}\rfloor-1.5}^{\lfloor y_{max}\rfloor+1.5}\sum_{m_z=\lfloor z_{min}\rfloor-1.5}^{\lfloor z_{max}\rfloor+1.5}c_{m_x}(m_x)e^{jk_xm_{x}}c_{m_y}(m_y)e^{jk_ym_{y}}c_{m_z}(m_z)e^{jk_zm_{z}}
\]

再把系数项单独拿出来：

\[Q(m_x,m_y,m_z)=\sum_{i=0}^{N-1}q_ic_{m_x}(m_x)c_{m_y}(m_y)c_{m_z}(m_z)
\]

这里的\(Q\)其实是一个shape为\((N_x,N_y,N_z)\)的张量，而\(m_x,m_y,m_z\)对应的是某一个格点的张量索引，每一个索引对应的张量元素都是通过系数函数计算出来的，有了这样的一个概念之后，再重写\(S(\mathbf{k})\)的函数：

\[S(\mathbf{k})=\sum_{m_x=\lfloor x_{min}\rfloor-1.5}^{\lfloor x_{max}\rfloor+1.5}\sum_{m_y=\lfloor y_{min}\rfloor-1.5}^{\lfloor y_{max}\rfloor+1.5}\sum_{m_z=\lfloor z_{min}\rfloor-1.5}^{\lfloor z_{max}\rfloor+1.5}Q(m_x,m_y,m_z)e^{j\mathbf{k}\cdot\mathbf{m}}
\]

我们会发现，这个插值出来的\(S(\mathbf{k})\)函数其实是在计算张量\(Q\)在\(\mathbf{k}\)处的傅里叶变换，那么就可以进一步简写\(S(\mathbf{k})\)的形式：

\[S(\mathbf{k})=VF_{\mathbf{k}}^{*}(Q)(m_x,m_y,m_z)
\]

其中\(F^{*}\)表示逆傅里叶变换，\(V\)表示逆傅里叶变换归一化常数。按照前面的4-格点拉格朗日插值法，此时得到的\(S(\mathbf{k})\)的值是一个shape为（4，4，4）的张量，这个张量的含义是64个格点分别对于倒格矢\(\mathbf{k}\)的贡献（插值出来的单个点电荷的作用效果）。那么类似的可以得到：

\[s(\mathbf{k})=VF_{\mathbf{k}}^{*}(Q)(m_x,m_y,m_z)F_{\mathbf{k}}(Q)(m_x,m_y,m_z)=V|F_{\mathbf{k}}(Q)(m_x,m_y,m_z)|^2
\]

代入到Ewald形式的长程相互作用项（可以参考这篇文章）中可以得到：

\[\begin{align*}
E^L&=\frac{1}{2k_xk_yk_z\epsilon_0}\sum_{|\mathbf{k}|>0}\frac{e^{-\frac{\sigma^2 k^2}{2}}}{k^2}s(\mathbf{k})\\
&=\frac{V}{2k_xk_yk_z\epsilon_0}\sum_{|\mathbf{k}|>0}\frac{e^{-\frac{\sigma^2 k^2}{2}}}{k^2}|F_{\mathbf{k}}(Q)(m_x,m_y,m_z)|^2
\end{align*}
\]

这就是Particle-Mesh-Ewald方法计算中计算长程相互作用势能的技巧。既然\(\mathbf{k}\)空间无法快速收敛，那就减少电荷分布项的计算复杂度，同样也可以起到大量节约计算量的效果。

短程相互作用项的截断

在前面Ewald求和的文章中我们介绍过，把静电势能的计算分成长程、短程和自我相互作用项之后，分别有不同的收敛形式。长程相互作用项已经通过上述章节完成了计算量的简化，另外还有一个短程相互作用项\(E^{S}\)，我们知道短程相互作用项关于原子实空间的间距是快速收敛的，并且在计算LJ势能的时候我们已经计算过一次给定cutoff截断的近邻表。那么，我们很容易考虑到引入近邻表的概念，直接利用这个近邻表对静电势能的短程相互作用项做一个截断。于是短程相互作用项可以写为：

\[\begin{align*}
E^S&=\sum_{\mathbf{n}}\sum_{i=0}^{N-2}\sum_{j=i+1}^{N-1}\frac{q_iq_j}{4\pi\epsilon_0|\mathbf{r}_j-\mathbf{r}_i+\mathbf{n}\mathbf{L}|}Erfc\left(\frac{|\mathbf{r}_j-\mathbf{r}_i+\mathbf{n}\mathbf{L}|}{\sqrt{2}\sigma}\right)+\sum_{|\mathbf{n}|>0}\frac{q_i^2}{4\pi\epsilon_0|\mathbf{n}\mathbf{L}|}Erfc\left(\frac{|\mathbf{n}\mathbf{L}|}{\sqrt{2}\sigma}\right)\\
&\approx \sum_{i,j\in \{Neigh\}}\frac{q_iq_j}{4\pi\epsilon_0|\mathbf{r}_j-\mathbf{r}_i|}Erfc\left(\frac{|\mathbf{r}_j-\mathbf{r}_i|}{\sqrt{2}\sigma}\right)
\end{align*}
\]

这里有个前提假设是\(d_{cutoff}<<L_{pbc}\)，所以略去了周期性盒子中其他盒子内的\(i\)电荷对中心盒子的\(\mathbf{r}_i\)处的作用项。

Particle-Mesh-Ewald

根据上面章节中得到的近似的远程相互作用项和短程相互作用项之后，我们可以重写PME(Particle-Mesh-Ewald)算法中的总静电势能为：

\[\begin{align*}
E&=E^S+E^L-E^{self}\\
&=\sum_{i,j\in \{Neigh\}}\frac{q_iq_j}{4\pi\epsilon_0|\mathbf{r}_j-\mathbf{r}_i|}Erfc\left(\frac{|\mathbf{r}_j-\mathbf{r}_i|}{\sqrt{2}\sigma}\right)\\
&+\frac{V}{2k_xk_yk_z\epsilon_0}\sum_{|\mathbf{k}|>0}\frac{e^{-\frac{\sigma^2 k^2}{2}}}{k^2}|F_{\mathbf{k}}(Q)(m_x,m_y,m_z)|^2\\
&-\frac{1}{4\pi\epsilon_0}\frac{1}{\sqrt{2\pi}\sigma}\sum_{i=0}^{N-1}q_i^2
\end{align*}
\]

总结概要

本文介绍了使用基于格点拉格朗日插值法的Particle Mesh Ewald算法，降低分子力场中的静电势能项计算复杂度的基本原理。静电势能的计算在Ewald求和框架下被拆分成了远程相互作用项和短程相互作用项，其中短程相互作用项关于实空间的点电荷间距快速收敛，而远程相互作用项在倒易空间慢速收敛。因此在远程相互作用的计算中，可以使用插值法降低单个倒易格点的计算复杂度，从而使得整体的远程相互作用项计算也能够快速收敛。

版权声明

本文首发链接为：https://www.cnblogs.com/dechinphy/p/pme.html

作者ID：DechinPhy

更多原著文章：https://www.cnblogs.com/dechinphy/

请博主喝咖啡：https://www.cnblogs.com/dechinphy/gallery/image/379634.html

参考链接

1. https://bohrium.dp.tech/notebooks/62979247598