使用Python解决Logistic方程

引言

在数学和计算机科学中，Logistic 方程是描述人口增长、传播过程等现象的一种常见模型。它通常用于表示一种有限资源下的增长过程，比如动物种群、疾病传播等。本文将带领大家通过 Python 实现 Logistic 方程的求解，帮助你更好地理解这一经典数学模型。

1.什么是 Logistic 方程？

Logistic 方程是一个非线性差分方程，常常用来描述在环境容量有限的情况下，种群、物种或其他生物体数量的变化过程。其基本形式为：$$\frac{dN}{dt} = rN(1 - \frac{N}{K})$$

其中

• N(t)是时间 t 时的种群数量。
• r 是增长率(即种群每单位时间的增长速度)。
• K 是环境的承载能力(最大种群数)。
• \(\frac{dN}{dt}\) 是种群数量随时间的变化率。

简单来说，Logistic 方程模拟的是种群在最初时快速增长，但随着种群接近环境承载上限，增长速度会逐渐减缓，最终趋于稳定。

2.Python 实现 Logistic 方程

我们通过 Python 来模拟 Logistic 方程的数值解。为了简化，我们假设种群的增长率 r 和承载能力 K 是已知的。接下来使用 Euler 方法(欧拉法)来近似计算每个时间步长上的种群数量。

1.初始化参数和变量

我们先定义 Logistic 方程所需要的参数，如增长率 r、承载能力 K、初始种群数量 \(N_0\) 以及模拟的时间步长和总时间。

# coding=utf-8
import matplotlib

matplotlib.use('Agg')
import numpy as np
import matplotlib.pyplot as plt

# 参数设置
r = 0.1  # 增长率
K = 1000  # 承载能力
N0 = 10  # 初始种群数量
T = 200  # 总时间
dt = 0.1  # 时间步长

# 计算步数
steps = int(T / dt)

2.使用 Euler 方法求解方程

在 Euler 方法中，我们将方程转化为离散形式，通过计算当前时刻的变化量来更新种群数量：\(N_{t+1} = N_t + \frac{dN}{dt} \times \Delta t\)

# 初始化种群数组
N = np.zeros(steps)
N[0] = N0

# 欧拉法求解Logistic方程
for t in range(1, steps):
    dN_dt = r * N[t-1] * (1 - N[t-1] / K)
    N[t] = N[t-1] + dN_dt * dt

3.绘制结果

通过 matplotlib 库，我们可以将种群数量随时间变化的结果可视化。

# 绘制种群数量随时间变化的图像
plt.plot(np.arange(0, T, dt), N)
plt.title('Logistic Growth Model')
plt.xlabel('Time')
plt.ylabel('Population Size')
plt.grid(True)
plt.savefig('Logistic.png')

输出结果

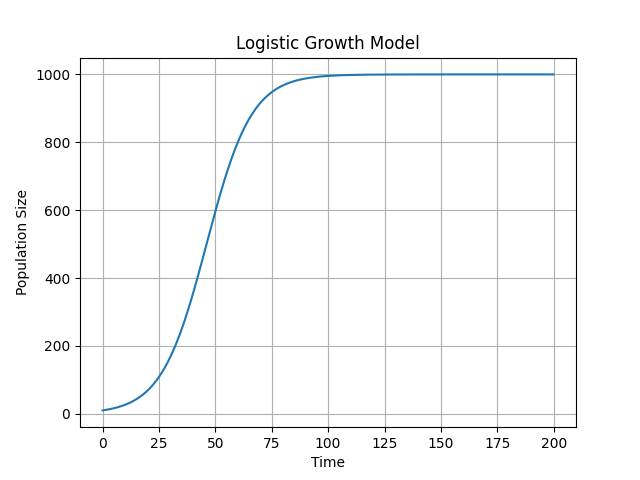
4.结果分析

在上述代码运行后，你将看到一个典型的 Logistic 曲线。种群数量在初期呈指数增长，但随着时间的推移，增长逐渐减缓，最终趋于承载能力 K 的上限。这个过程非常符合自然界中很多生物种群的增长模式。

总结

通过 Python，我们可以很容易地实现 Logistic 方程，并利用数值方法(如 Euler 法)来逼近其解。这个模型不仅仅适用于生物学领域，还广泛应用于流行病学、经济学等多个学科。理解并掌握 Logistic 方程的求解，对于分析实际问题、制定合理策略都有着重要的意义。

希望通过这篇文章，你能够更清晰地理解 Logistic 方程以及如何使用 Python 来进行模拟。如果你对更复杂的数学模型和 Python 实现感兴趣，可以继续深入学习更多的数值解法和优化算法！