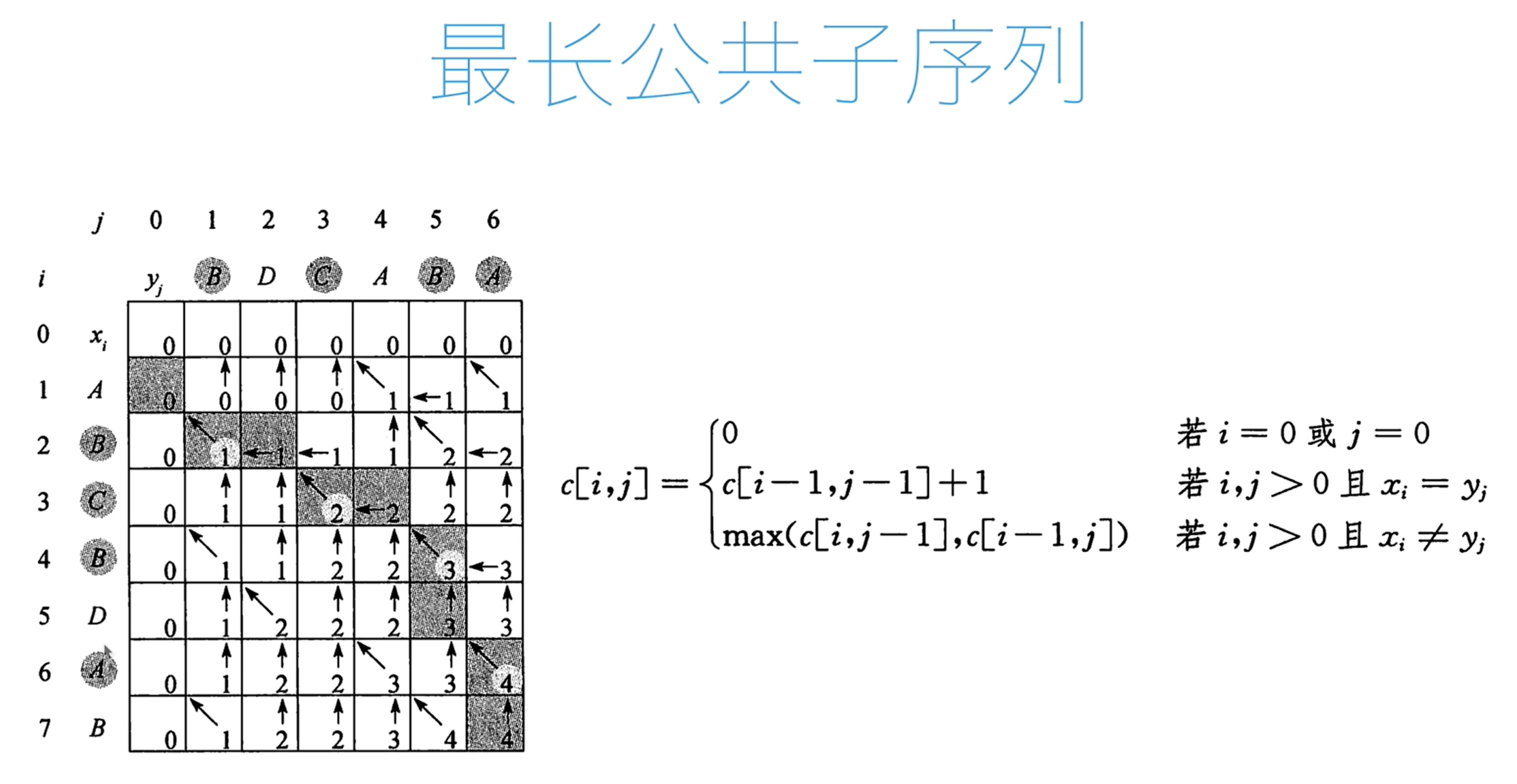
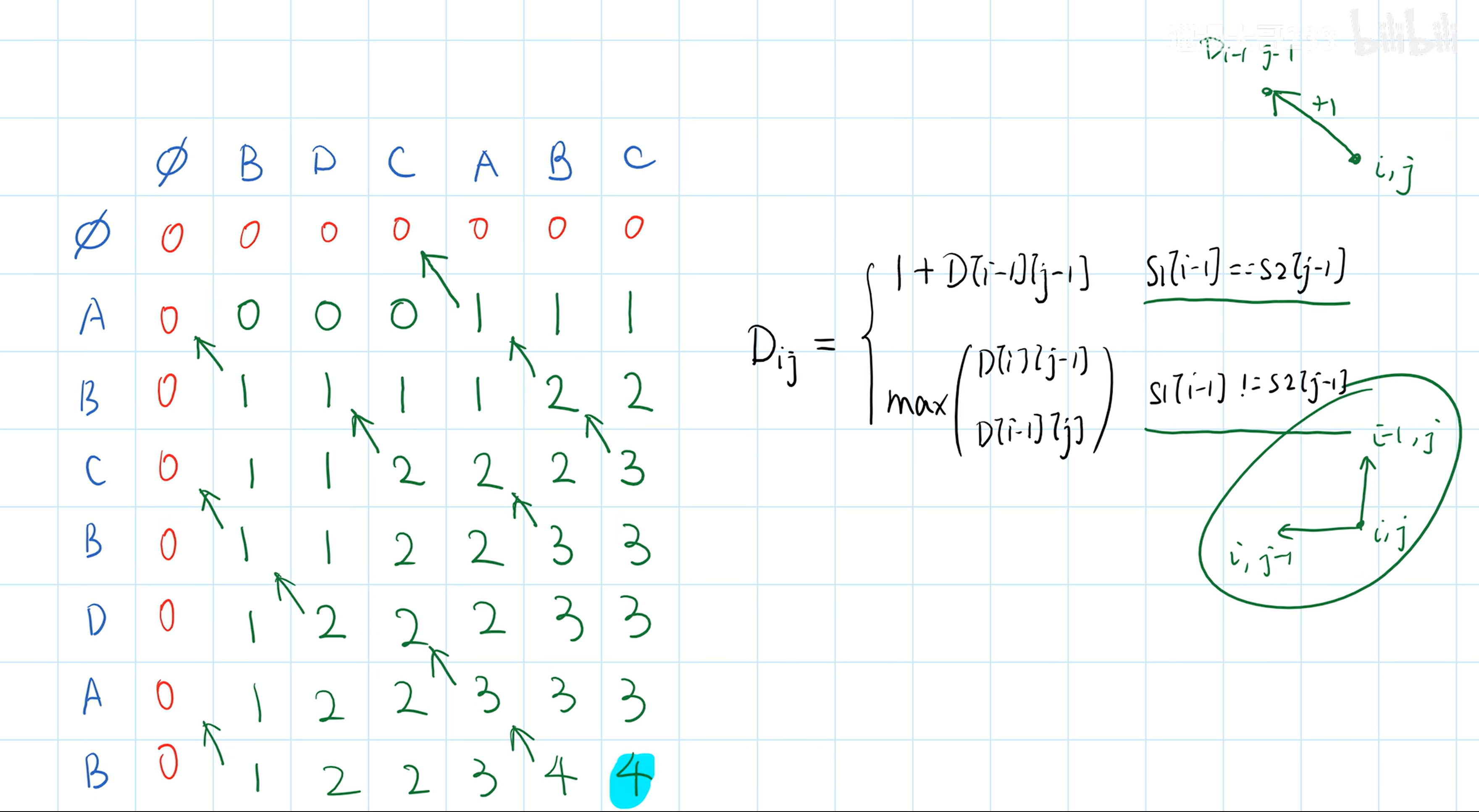动态规划--最长公共子序列（ LCS 问题）

博客地址：https://www.cnblogs.com/zylyehuo/

• 
• 
• 
• 
• 
• 
• 

# -*- coding: utf-8 -*-

# 最长公共子序列的长度
def lcs_length(x, y):
    m = len(x)
    n = len(y)
    c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if x[i - 1] == y[j - 1]:  # i j 位置上的字符匹配的时候，来自于左上方+1
                c[i][j] = c[i - 1][j - 1] + 1
            else:
                c[i][j] = max(c[i - 1][j], c[i][j - 1])
    for _ in c:
        print(_)
    return c[m][n]

print("==========================最长公共子序列的长度==========================")
print(f'最长公共子序列的长度为：{lcs_length("ABCBDAB", "BDCABA")}')

def lcs(x, y):
    m = len(x)
    n = len(y)
    c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    b = [[0 for _ in range(n + 1)] for _ in range(m + 1)]  # 1 左上方 2 上方 3 左方
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if x[i - 1] == y[j - 1]:  # i j 位置上的字符匹配的时候，来自于左上方+1
                c[i][j] = c[i - 1][j - 1] + 1
                b[i][j] = 1
            elif c[i - 1][j] > c[i][j - 1]:  # 来自于上方
                c[i][j] = c[i - 1][j]
                b[i][j] = 2
            else:
                c[i][j] = c[i][j - 1]
                b[i][j] = 3
    return c[m][n], b

def lcs_trackback(x, y):
    c, b = lcs(x, y)
    for _ in b:
        print(_)
    i = len(x)
    j = len(y)
    res = []
    while i > 0 and j > 0:
        if b[i][j] == 1:  # 来自左上方=>匹配
            res.append(x[i - 1])
            i -= 1
            j -= 1
        elif b[i][j] == 2:  # 来自于上方=>不匹配
            i -= 1
        else:  # ==3 来自于左方=>不匹配
            j -= 1
    return "".join(reversed(res))

print("===============================最长公共子序列===============================")
print(lcs_trackback("ABCBDAB", "BDCABA"))