【2020.11.30提高组模拟】柱形图(histogram) 题解

题意简述

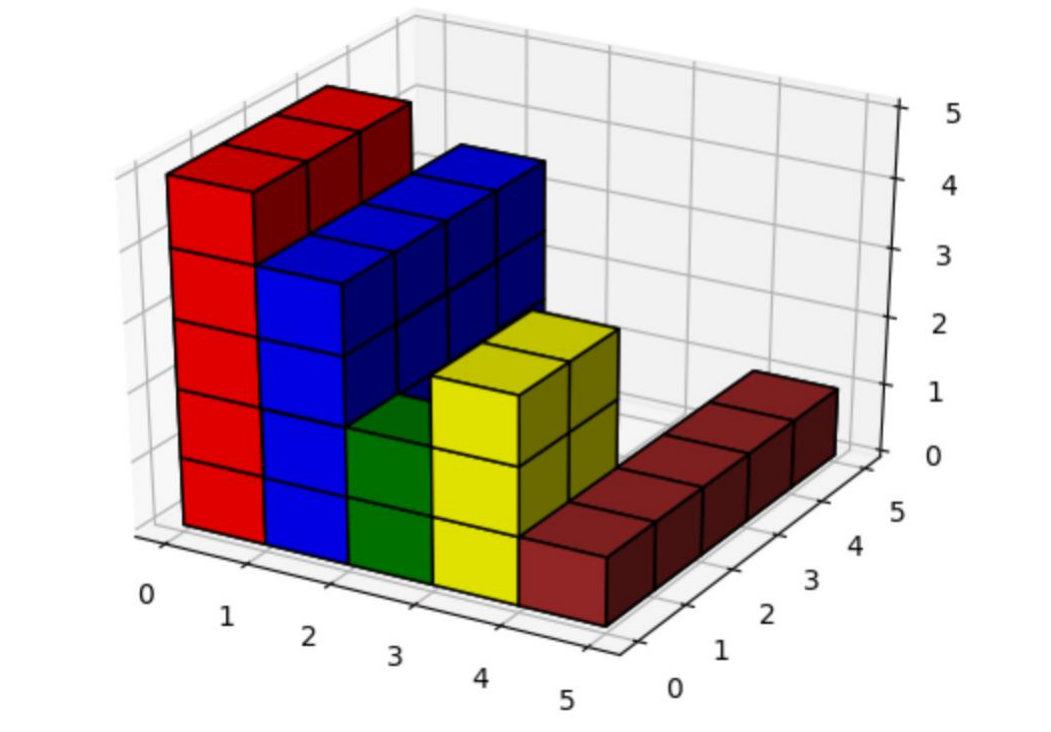
有\(n\)个长方体并排这样放着，每种颜色的长方体的宽度都为\(1\)，高\(a_i\)长\(b_i\)。

求在这些长方体内部最大能够放入的长方体的体积。

\(n\le200000\).

Solution

这个问题可以在\(O(n\log^2n)\)的时间复杂度内解决。

设\(f(i,j)=\min(a_i,\dots,a_j),g(i,j)=\min(b_i,\dots,b_j)\)。

这个问题就被转化成了找到一个区间\([i,j]\)使得\(\max f(i,j)\cdot g(i,j)\cdot (j-i+1)\)。

考虑分治\((divide-and-conquer)\)。

\(solve(lo,hi)\)将找到区间\([lo,hi]\)中横跨区间\(mid\)的最优的区间。他将递归调用\(solve(lo,mid-1)\)和\(solve(mid+1,hi)\)。

为了递归合并区间，我们设\([l,r]\)是一个\(l\in[lo,mid],r\in[mid,hi]\)的区间。我们考虑四种情况：

\(f(l,r)\)和\(g(l,r)\)都是由左半部分决定，即\(f(l,r)=f(l,mid),g(l,r)=g(l,mid)\).
\(f(l,r)\)和\(g(l,r)\)都取决于右半边，即\(f(l,r)=f(mid,r),g(l,r)=g(mid,r)\).
\(f(l,r)\)取决于左侧，\(g(l,r)\)取决于右侧.
\(f(l,r)\)取决于右侧，\(g(l,r)\)取决于左侧.

情况\(1/2\)是类似的，情况\(3/4\)是类似的，所以我们只需要考虑情况\(1/3\)。

情况\(1\)

\(f(l,r)\)和\(g(l,r)\)都是由左半部分决定

注意到这意味着\(f(l,mid)\le f(mid,r),g(l,mid)\le g(mid,r)\).

我们可以使用双指针法在\(O(hi-lo)\)的时间内解出来，所以总时间复杂度就变成了\(O(n\log n)\).

情况\(3\)

\(f(l,r)\)取决于左侧，\(g(l,r)\)取决于右侧

注意到这意味着\(f(l,mid)\le f(mid,r),g(l,mid)\le g(mid,r)\).

这个就没有情况\(1/2\)那样可以在\(O(n\log n)\)内解出来。

它存在\(O(n\log^2n)\)的解法，我们将首先介绍一种\(O(n\log^3n)\)的解法。

\[\begin{aligned}
f(l,r)\cdot g(l,r)\cdot (r-l+1)&=f(l,mid)\cdot g(mid,r)\cdot (r-l+1)\\
&=f(l,mid)\cdot (-l+1)\cdot g(mid,r)+f(l,mid)\cdot g(mid,r)\cdot r\\
&=\langle(f(l,mid)\cdot (-l+1),f(l,mid)),(g(mid,r),g(mid,r)\cdot r)\rangle
\end{aligned}
\]

其中\(\langle(a,b),(c,d)\rangle\)表示向量\((a,b)\)和\((c,d)\)的点积。

注意到第一个向量仅仅依赖于\(l\)，第二个向量仅仅依赖于\(r\).

对于一个固定的\(l\)，我们希望找到一个\(r\in[a(l),b(l)]\)使得这两个向量的点积最大。如果\(r\)不属于那个区间，我们可以计算第二个点集的凸包，然后用三分查找找到对于每个\(l\)的最优的\(r\)。但是现在，我们可以对这些点按照它们的横坐标排序，然后建一棵线段树，这棵线段树的每个节点都记录着相应的凸包。所以对于每个\(l\)我们将会查看线段树上的\(O(\log n)\)个节点，然后以单次的时间在每个节点对应的凸包内做三分查找。这给我们带来了一个\(O(n\log^3n)\)的算法，因为我们需要再用一个分治统计答案。

现在我们想要摆脱二分，注意到点\(f(l,mid)\cdot (-l+1,1)\)随着\(l\)增加而向逆时针移动，所以凸包上的极值点也会向逆时针移动，对于线段树上的每个节点，我们可以在\(O(n)\)的时间内完成一次询问，通多记录上次询问的极值点的指针的方式。这给我们带来了一个\(O(n\log^2n)\)的方法。