算法学习记录-查找——折半查找(Binary Search)
以前有个游戏,一方写一个数字,另一方猜这个数字。比如0-100内一个数字,看谁猜中用的次数少。
这个里面用折半思想猜会大大减少次数。
步骤:(加入数字为9)
1.因为数字的范围是0-100,所以第一次猜50(100的一半)
2.缩小范围到0-50,根据对方回应数大了,再猜25(50的一半)
3.缩小范围到0-25,对方回应数大了,再猜13
4.缩小范围到0-13,对方回应数大了,再猜7
5.缩小范围到7-13,对方回应数小了,再猜10
6.缩小范围到7-10,对方回应数大了,再猜9,中
真是比较差的情况,最差的情况这样逐次缩小到最后一个数,应该是需要猜7次。
这就是折半查找思想,非常的简单,但是有个前提,所要查找的记录序列是有序数列。
知道了思想,程序就好写了。
看图:查找7的过程
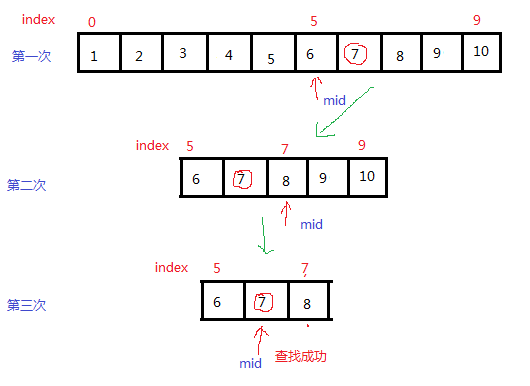
折半查找程序:
int BinSerch(myDataType *ary,int len,int val)
{
int low,mid,high;
low = ;
high = len-; while(low <= high)
{
mid = (high+low)/;
if (val == ary[mid])
{
return mid;
}
else if (val > ary[mid])
{
low = mid+;
}
else if (val < ary[mid])
{
high = mid-;
} }
return -;
}
完整代码:
#include "stdafx.h" typedef int myDataType;
//myDataType src_ary[10] = {9,1,5,8,3,7,6,0,2,4};
//myDataType src_ary[10] = {1,2,3,4,5,6,7,8,9,10};
myDataType src_ary[] = {,,,,,,,,,};
void prt_ary(myDataType *ary,int len)
{
int i=;
while(i < len)
{
printf(" %d ",ary[i++]);
}
printf("\n");
} void bubble_sort (myDataType *ary,int len)
{
int i,j;
for (i=;i<len;i++)
{
for (j=len-;j>=i;j--)
{
if (ary[j] > ary[j+])
{
myDataType temp = ary[j];
ary[j] = ary[j+];
ary[j+] = temp;
}
}
}
}
int BinSerch(myDataType *ary,int len,int val)
{
int low,mid,high;
low = ;
high = len-; while(low <= high)
{
mid = (high+low)/;
if (val == ary[mid])
{
return mid;
}
else if (val > ary[mid])
{
low = mid+;
}
else if (val < ary[mid])
{
high = mid-;
} }
return -;
} int _tmain(int argc, _TCHAR* argv[])
{
printf("before sort:\n");
prt_ary(src_ary,); bubble_sort(src_ary,); printf("after sort:\n");
prt_ary(src_ary,); int idx = BinSerch(src_ary,,);
if (- == idx)
{
printf("no value in array!\n");
}
else
{
printf("index = %d\n",idx);
} getchar();
return ;
}
测试结果:
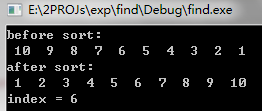
算法学习记录-查找——折半查找(Binary Search)的更多相关文章
- 算法与数据结构基础 - 折半查找(Binary Search)
Binary Search基础 应用于已排序的数据查找其中特定值,是折半查找最常的应用场景.相比线性查找(Linear Search),其时间复杂度减少到O(lgn).算法基本框架如下: //704. ...
- 算法学习记录-查找——二叉排序树(Binary Sort Tree)
二叉排序树 也称为 二叉查找数. 它具有以下性质: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值. 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值. 它的左.右子树也分别 ...
- C语言查找算法之顺序查找、二分查找(折半查找)
C语言查找算法之顺序查找.二分查找(折半查找),最近考试要用到,网上也有很多例子,我觉得还是自己写的看得懂一些. 顺序查找 /*顺序查找 顺序查找是在一个已知无(或有序)序队列中找出与给定关键字相同的 ...
- python3--算法基础:二分查找/折半查找
算法基础:二分查找/折半查找 #!/usr/bin/env python # -*- coding:utf-8 -*- # 算法基础:二分查找/折半查找 def binarySearch(dataSo ...
- 算法学习记录-查找——平衡二叉树(AVL)
排序二叉树对于我们寻找无序序列中的元素的效率有了大大的提高.查找的最差情况是树的高度.这里就有问题了,将无序数列转化为 二叉排序树的时候,树的结构是非常依赖无序序列的顺序,这样会出现极端的情况. [如 ...
- 顺序查找 && 折半查找
顺序查找 算法描述 顺序比较即可. 平均查找长度 (n+1)/2, 其中n为表长 ...
- swift版 二分查找 (折半查找)
二分查找作为一种常见的查找方法,将原本是线性时间提升到了对数时间范围之内,大大缩短了搜索时间,但它有一个前提,就是必须在有序数据中进行查找.废话少说,直接上代码,可复制粘贴直接出结果! import ...
- 72【leetcode】经典算法- Lowest Common Ancestor of a Binary Search Tree(lct of bst)
题目描述: 一个二叉搜索树,给定两个节点a,b,求最小的公共祖先 _______6______ / \ ___2__ ___8__ / \ / \ 0 _4 7 9 / \ 3 5 例如: 2,8 - ...
- 【学习记录】二分查找的C++实现,代码逐步优化
二分查找的思想很简单,它是针对于有序数组的,相当于数组(设为int a[N])排成一颗二叉平衡树(左子节点<=父节点<=右子节点),然后从根节点(对应数组下标a[N/2])开始判断,若值& ...
随机推荐
- 微信支付(java版本)_支付结果通知
应用场景: 支付完成后,微信会把相关支付结果和用户信息发送给商户,商户需要接收处理,并返回应答. 对后台通知交互时,如果微信收到商户的应答不是成功或超时,微信认为通知失败,微信会通过一定的策略定期重新 ...
- MyBatis学习总结(一)
MyBatis,是一个支持普通SQL查询,存储过程和高级映射的优秀持久层框架.MyBatis消除了几乎所有的JDBC代码和参数的手工设置以及对结果集的检索封装.MyBatis可以使用简单的XML或注解 ...
- ios获取数据之encodeURI 和 decodeURI
在APP开发过程中,免不了要进行ios的数据处理,在ios传递数据的过程中,会出现JSON数据获取不到的情况,这时候就轮到encodeURI 和 decodeURI出马了. 1.encodeURI,d ...
- 最具士兵突击实战类型的JavaScript
JavaScript实战一书的基础知识部分帮助读者快速踏入JavaScript领域之门,jQuery部分帮助读者随心所欲地去工作,HTML5部分帮读者搭上时代的班车,Node.JS则可以让读者屹立在技 ...
- HDU 1850 Being a Good Boy in Spring Festival 在春节做乖孩子(Nim博弈,微变形)
题意: 思路: 如果全部扑克牌数目异或的结果ans为0,则必输,输出0.否则,必须要给对方一个P状态,可以对所有扑克堆进行逐个排查,将ans^a[i]就可以得到除了a[i]之外其他扑克数的异或结果tm ...
- 洛谷——普及练习场 普及组选手可冲刺训练,提高组选手亦可在此巩固基础。(Loading...)
简单的模拟 关卡2-1,6 道题 开始普及组的训练!所谓模拟,就是直接根据题意编写,思维难度简单. //T1 铺地毯 #include <cstdio> #define N 10005 i ...
- Linq语法学习_增删篇。
关键词: select from where in into join on equals orderby descending thenby Table<TEntity> Default ...
- 清理winsxs文件夹(系统更新文件)的第三方工具
工具名称(第三方): Windows Update Clean Tool 下载地址: http://www.xiazaiba.com/html/24145.html http://dx5.xiazai ...
- python基础教程总结6——类
1. 如何定义一个类 在进行python面向对象编程之前,先来了解几个术语:类,类对象,实例对象,属性,函数和方法. 类是对现实世界中一些事物的封装,定义一个类可以采用下面的方式来定义: class ...
- HDU - 5457 Hold Your Hand (Trie + 最小割)
Hold Your Hand Time Limit: 1500/1000 MS (Java/Others) Memory Limit: 65535/102400 K (Java/Others)T ...
