CF-1096C Polygon for the Angle

CF-1096C Polygon for the Angle

https://codeforces.com/contest/1096/problem/C

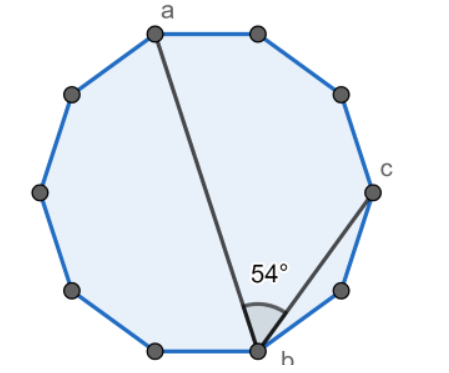
题意：给一个角度ang(1<=ang<=180) 然后输出如图所示规则的最小正n边形的边数

分析：abc三点构成一个三角形，而三角形内角的比例就对应于它们各自对应的那段边数比。如图，54度对应三份，剩下的分别对应五份和两份。

所以，对于任意一个角度ang，先求出g=gcd(ang,180)，即每一边可以对应多少度，然后 n=180/g 即为正n边形的边数，wait wait！是不是有点太快了，别忘了我们的前提条件，我们是用三角形内角比例等于对应边数比得到的结论，我们要让它满足能够组成三角形这一条件，所以发现当 ang/180==(n-1)/n 时（想一想为什么是这样），就无法组成三角形（因为只剩下一份了，不够与ang组成三角形），这个时候只需将 n乘以2即可。

#include <bits/stdc++.h>
using namespace std;
int T,ang,n;
int main()
{
	cin>>T;
	while(T--)
	{
		cin >> ang;
		int n = 180/__gcd(ang,180);
		if(ang * n / 180 == n-1){
			n*=2;
		}
		cout << n << endl;
	}
}