面向对象OO第一单元三次作业总结

（一）第一单元的作业围绕着多项式的求导，从简单到复杂，主要的要求是

　　　　作业一：只有两种格式的因子：带符号整数（+02）和幂函数（x^+02）。

　　　　作业二：在作业一的基础上添加了：sin(x)和cos(x)以及首项的第一个因子为+1或-1可以省略“1”

　　　　作业三：在作业二的基础上增加了 “表达式因子”的概念：用括号括起来的整个表达式，如（x+sin(x)）,另外sin()和cos()的括号中可含所有因子，如sin(+2),sin(x^2),sin(sin(x)),sin((x+x))

（二）我三次作业的思路：

　　　　作业一：由于只有两种固定格式的因子(+1，+x^+1)，所以我用的是状态机，一共分了九个状态，并同时分别统计系数和指数，然后统一求导。我的主要的方法行数超过了60行——但如果我把判断格式合法性和统计系数指数分开成两个方法的话，就不会超了

　　　　作业二：由于增加了sin(x)和cos(x)，而且在作业一中我的主要的方法的长度就远远超过了规定的60行，分开判断与统计也会超，所以我用了正则表达式来判断输入的合法性，正则表达式分为：

　　　　　　sin_cos:“[ \\t]*((sin)|(cos))[ \\t]*\\([ \\t]*x[ \\t]*\\)([ \\t]*\\^[ \\t]*[+-]?\\d+[ \\t*])?”

　　　　　　x          :"[ \\t]*x[ \\t]*(\\^[ \\t]*[+-]\\d+)?"

　　　　　　d         :"[ \\t]*[+-]?\\d+"

　　　　　　整串的判断就为： “([ \\t]*[+-]?(sin_cos|x|d)[ \\t]*(\\*(sin_cos|x|d)[ \\t]*)*)+”，即将整串分为 “（首个因子（*后面的因子——可能没有））+”的格式。

　　　　　　然后处理字符串，让各个加数能以“+”直接被“split”出来，各个乘数能以“*”直接被split出来，再一个个分别求导。

　　　　　　由于格式固定，正则表达式真的超好用，不过有时候爆栈就不好用了。

　　　　作业三：表达式不固定了——但还是有套路——factor,sin((factor))。由于目前java的正则表达式不能判断所有的括号是否匹配，所以我选择的是“逐层判断”，先将字符串转换成数组，逐一将最外层的括号及其里面的东西转换成一个字符“？”（好吧这非常不“面对对象”），然后判断当前表达式是否为这四种“因子”：

　　　　　　sin_cos: sin?形式（空格、指数之类的与上面的一致，就不写了，下面同）

　　　　　　x:与上面一致

　　　　　　d:与上面一致

　　　　　　表达式因子：\\?

　　　　　　所以整串的表达式判断类似于：“([+-]?((sin_cos)|x|d|(\\?))(\\*((sin_cos)|x|d|(\\?))))+*”（空白字符及最开头的+1省略之类的就不表示出来了）

　　　　到这里可能会问：那括号里面的东西不合法怎么办？我是这样做的：

　　　　　　在判断最外层的合法后：

　　　　　　将当前的整串交给负责“初次求导”的“求导一号”去办，它们会将整串遍历以分出各个加数、然后将各个加数送去“求导二号”，

　　　　　　“求导二号”会将当前送来的加数分成各个乘数——有sin()形式，有x^2形式，有+2形式，有（）形式，然后又将这些乘数送给对应的“各小求导部门”——专门负责求sin()形式的、专门负责求x^2形式的、专门负责求（）形式的，（至于纯数字的乘数，会让它保留在“求导二号”，等大家都求完导回来后再和大家汇合）。另外在这个方法里面我还将当前表达式中所有的sin()形式的因子和()形式的因子分别统计成了两个动态数组，记为A、B，用途我后面再说。

　　　　　　而“各小部门”又会先各自检查自己的字符串的“最外层”是否合法——主要是sin（）形式和（）形式的——因为它们里面的还要求导嘛，而且x形式的之前已经判断过了，于是乎，它们在提取出最外层括号里面的表达式之后，就将剥出来的“小表达式”送入下一层的判断（一样的类、一样的方法——“（）”变成“？”那个）、小表达式又会经过求导一号、求导二号、各小部门。。。

　　　　　　直到最后的表达式不含括号后，将其中规中矩地求完导，然后返回上一级。

　　　　　　然而，这里往下传递似乎很好想，可是，下一级的求完导后要怎样和上一级的汇合呢？

　　　　　　首先，我介绍下自己设定的类Val——包括 xs(系数),zs(x的指数),动态数组一号（各种奇怪的sin()、cos()及他们各自的指数，是的，这里面又有一个小类Valsin），动态数组二号（各种奇奇怪怪的（factor）形式），（毕竟其他的在求导时它们是不能变的嘛）。

　　　　　　所以，在每一个部门里面求完导之后都会返回一个ArrayList(Val),然后会一个一个取出这里面的东西，和当前的汇合——xs相乘，zs相加，（之前统计的两个数组的作用出来了——）动态数组一号将当前一级的A中的所有Valsin一个一个添加进去，动态数组二号将当前一级的B中的所有（factor）一个一个加入，然后再一层层返回。。。最后输出时，将当前的每一个Valsin一个个按 xs,zs arrayList(Valsin),arrayList(string)格式输出就行了。

　　　　　　是的，我没有做优化。。。

　　　　　　所以呢，结果就是我被hack了9个点。。。9个。。9.。。原因是在求sin(（factor）)形式、剥离里面的factor时由于没处理当，要么多了一个“）”要么只去掉了两头的空格，以及在里面判断是（factor）还是x^+2还是+2还是sin（）时忘了【+-】？的“？”。好我马上分享我的bug“历史”。

（三）我三次作业被查出来的bugs和我的“hack手段”:

　　　　　　第一次：荣幸！由于用了状态机，各方面钉得死死的，我的“和平室友们”没有hack到我，不过我也只是用了边界数据——超长的表达式使他们的正则爆栈hack到了他们。

　　　　　　　　　　hack手段：查代码，主要是看正则表达式是否写错，比如[ \\t]*写成[ \\t]+的，或者用超长数据检测（在允许的范围内）

　　　　　　　　　　总结：第一次由于模式少、格式严格变动少，利用状态机或正则表达式很容易避免"WRONG FORMAT"的判断出错，不过爆栈是后话，我会在后面阐述为啥能爆栈

　　　　　　第二次：由于字符串的处理出了问题：对于已经合法的字符串，我的处理步骤是：

　　　　　　　　　　　　1，去掉所有空白字符；

　　　　　　　　　　　　2，将所有的"--"和“++”换成“+”；

　　　　　　　　　　　　3，将所有的“-+”以及不是“^-”以及不是“*-”以及不是“+-”的的带有“-”的换成“+-”；

　　　　　　　　　　　　4，将“^+”换成“+”，将“*+”换成“+”。

　　　　　　　　　　好吧我想已经看出问题了：第二步就将“--”“++”处理了的话，到第三步如果形成了“+--”形式的也不会再管了——而且我后面的处理也只是按照“+”分割，而且分割带符号整数和其它格式的因子时也只是“[+-]?\\d+”，然后“--d+”格式的就不会被读入并统计，输出结果永远为0.

　　　　　　第三次：我的第三次及其惨烈——由于字符串的处理没有到位：带括号的式子没有“.trim()”去掉最外层括号两边的空白字符就直接切割“substring(1,length-1)”,导致多出一个“）”或“（”或“（）”，进入下一级时就会直接“WRONG FORMAT！”，以及正则表达式的出错:sin、cos中判断x^+01形式时“[+-]?”没有“？”，导致对于cos(x^4)我直接是"WRONG FORMAT!"（因为不是cos(x^+4)）.

　　　　　　　　　　hack手段：由于我所在room的人的思路都差不多，都是按照“树结构”，所以我主要是看他们的代码，看字符串的处理、正则表达式、以及整合时有没有漏掉什么。

　　　　　　　　　　总结：根据互测和公测的数据，我的bug出现和结构无关，即总体思路还是没有错的（但是很“面对过程”）；另外，判断、处理字符串这里面真的要非常仔细，很容易出错。

（四）重构：

　　　　第一次：格式的判断会用正则表达式，而且统计xs(系数)，zs(指数)也会直接用matcher直接抓。

　　　　第二次：原有思路不变，但会设置存储时用harshmap类型存储——将x,sin(x),cos(x)三者的指数作为key

　　　　第三次：尽量转化为接口和继承。如果按我原来的思路，我只能把“各小求导部分”用一个接口合了，再各种重写,sin()和cos()的可以用一个继承实现

（五）一些数据

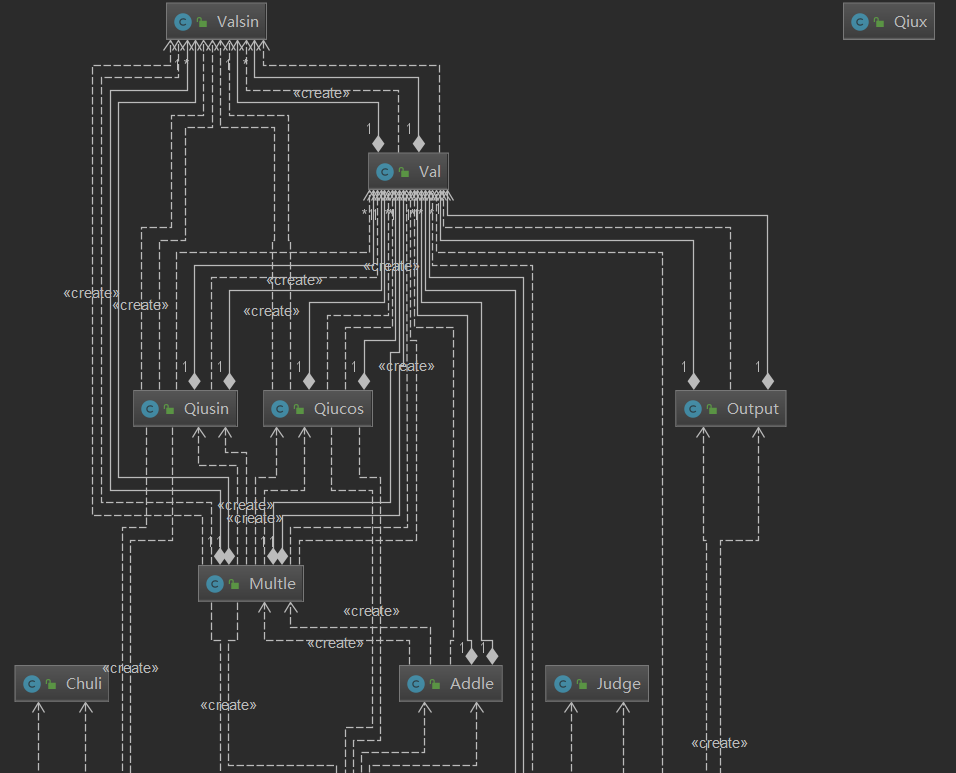
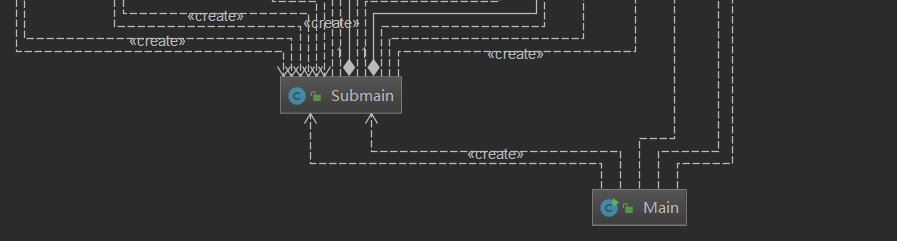
另外，第三次作业的类图如下，自底向上为main,submain——每次剥离除了新的表达式就进入sunmain，它会进行判断、进入加数求导、乘数求导、各小部门求导等行为

　　Addle类：加数分解、求导；Multle类：乘数分解求导；Qiusin:(sin()求导);Qiucos(cos()求导)；Qiux类：x^+1求导；Val类；Valsin类

另外还有一些数据：

第三次的：

　　各方法：

　

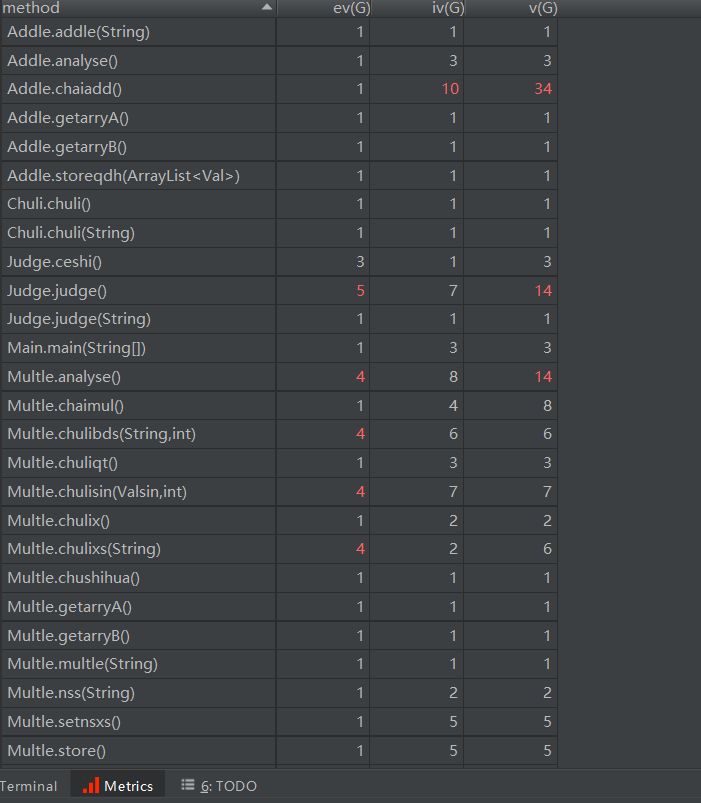
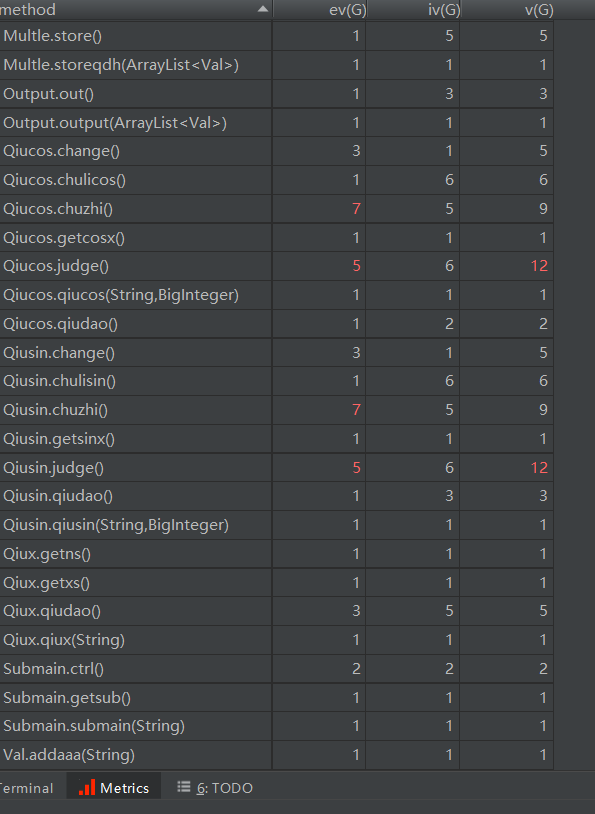
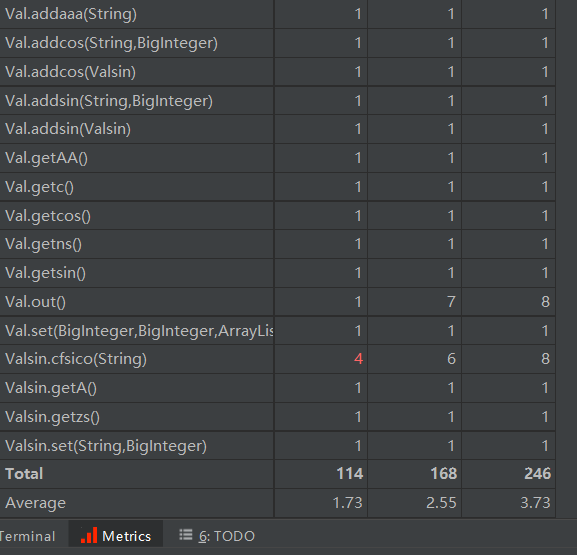
　　各类：

　

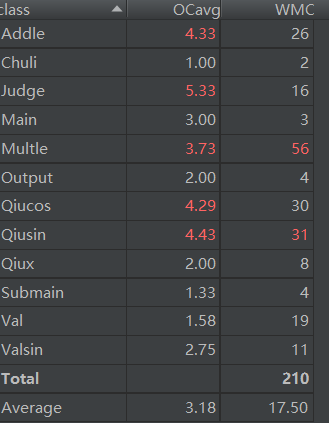
第二次的：

　　各方法：

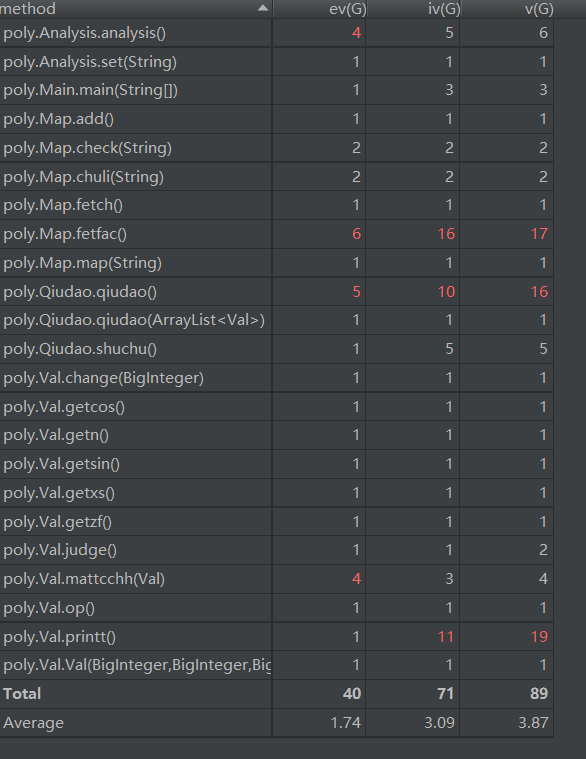
　　各类：