BZOJ2818 与 BZOJ2301【euler，线性筛，莫比乌斯】

题目大意：

　　给一个范围[1,n]，从中找出两个数x,y，使得gcd(x,y)为质数，问有多少对（x,y有序）

解法：

　　不难，欧拉函数练手题，可以定义集合P ={x|x为素数}，那么我们枚举gcd(x,y)可能等于的情况，对于任意p∈P可以得到：gcd(k1·p,k2·p) = p，当且仅当gcd(k1,k2) =1;那么我们就只需要枚举所有的k1,k2了。不妨设k1>k2，那么给定k1，k2的个数就是phi(k1),因为有序，所以给phi*2，但是，这样是否漏算了呢？没错，漏算了（1,1），补上就行了，那么这个的答案就是计算下面那个表达式。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　稍有常识的人就会看出，如果我们的坦克再前进一步(大雾)要算这个式子，复杂度是O(n^2)的，我们分析一下复杂度主要消耗再哪里。

　　1.算phi

　　　　如果我们用暴力公式，也就是的话，复杂度显然是很高的，全算出来高达（不是那个高达）O(n*sqrt(n))，这样的复杂度在1e7内是无法忍受的，所以我们　

　　　　必须另外想办法，下面我引入三个很厉害东西：

　　　　　　1.当p∈P时，phi(p) = p-1；

　　　　　  2.如果i mod p = 0, 那么 phi(i * p)=p * phi(i)，证明略，其实我也不会证

　　　　　  3.若i mod p ≠0,  那么 phi( i * p )=phi(i) * ( p-1 ) ；

　　　　有了这三个就容易写出线性的求euler函数了。

　　2.二重循环

　　　　里面那一重循环可以在外面递推乱搞，自己想，或者看我代码。

　　那么这个的复杂度就降为了O(n);

3.下面是代码

　　

 #include<bits/stdc++.h>
 using namespace std;
 int flag[],p[],tot;
 int phi[];
 void get_p(int end){
     for(int i=;i<=end;i++)
         flag[i] = ;
     for(int i=; i<=end; i++){
         if(flag[i]==){
             p[++tot]=i;
             phi[i] = i-;
         }
         for(int j=; j<=tot && p[j]*i<=end; j++){
             flag[p[j]*i]=;
             if(i%p[j]==){
                 phi[i*p[j]] = p[j] * phi[i]; //欧拉函数的特性
                 break;
             }else phi[i*p[j]] = (p[j]-) * phi[i];
         }
     }
 }
 long long f[];

 int main(){
     int n;
     cin >> n;
     get_p(n);
     f[] = ;
     for(int i=;i<=n;i++){
         f[i] = f[i-] +phi[i]*;
     }
     long long ans = ;
     for(int i=;i<=tot;i++){
         ans = ans+f[n/p[i]];
     }
     cout<<ans;
     return ;
 }

4.拓展

　　这个问题就这么轻易的解决了，但是我们稍加思考，就能想到它的一个变式：

　　变式链接： bzoj2301

　　给一个范围[l,n],[p,m],定义x,y，x∈[1,n],y∈[1,m]，使得gcd(x,y)=k，问有多少对（x,y无序）。

　　对于这道题，我们不得不引入新的概念，莫比乌斯反演：

　　其内涵主要是下面这个公式，其中mu是莫比乌斯函数，其定义为：

　　ki表示x的唯一分解后每个质数的次数。µ函数还有一个性质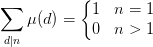

　　上面的莫比乌斯反演公式我们还有一种表达方法,本题要用的就是这个。

5.解决

　　可设f(x)表示gcd(a,b)=x的个数，F(x)表示满足x|gcd(a,b)的个数。那么我们可以考虑把区间分为两部分，对于[l,n]，我们可以将它分为[1,n]-[1,l]+{l}（又不是搞数学那么讲究干嘛），然后我们先计算在[1,n]中有多少个a是x的倍数，容易得到这个数字为n/x。同理我们可以求得在[1,l]中有l/x个，在[1,m]中有m/x个，在[1,p]中有p/x个。这样我们就容易得到在[l,n]这个闭区间中有s1=(n/x-l/x+[l|x])注意，这里的[l|x]表示的是下面的意思。同样，我们也可以得到在[p,m]中有s2=(m/x-p/x+[p|x])。那么F(x) =s1*s2个（乘法原理）。

 if(x % i == )
     return ;
 else
     return ;

并且我们还能得到另一个式子　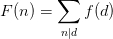　,我们的目的是要求f(k)，那么由这个式子和莫比乌斯反演公式可以得到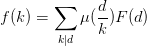，，嗯，我写一下看看提交上去会不会超时哈。