[Scikit-learn] 1.2 Dimensionality reduction - Linear and Quadratic Discriminant Analysis

Ref: http://scikit-learn.org/stable/modules/lda_qda.html

Ref: http://bluewhale.cc/2016-04-10/linear-discriminant-analysis.html

Ref: http://blog.csdn.net/lizhe_dashuju/article/details/50329663 【该系列，作者很用心，讲得很通透】

线性判别分析(Linear Discriminant Analysis)简称LDA，是分类算法中的一种。

LDA通过对历史数据进行投影，以保证投影后同一类别的数据尽量靠近，不同类别的数据尽量分开。并生成线性判别模型对新生成的数据进行分离和预测。

一、与PCA的几点不同

出发思想不同。PCA主要是从特征的协方差角度，去找到比较好的投影方式，即选择样本点投影具有最大方差的方向；而LDA则更多的是考虑了分类标签信息，寻求投影后不同类别之间数据点距离更大化以及同一类别数据点距离最小化，即选择分类性能最好的方向。
学习模式不同。PCA属于无监督式学习，因此大多场景下只作为数据处理过程的一部分，需要与其他算法结合使用，例如将PCA与聚类、判别分析、回归分析等组合使用；LDA是一种监督式学习方法，本身除了可以降维外，还可以进行预测应用，因此既可以组合其他模型一起使用，也可以独立使用。
降维后可用维度数量不同。LDA降维后最多可生成C-1维子空间（分类标签数-1），因此LDA与原始维度数量无关，只有数据标签分类数量有关；而PCA最多有n维度可用，即最大可以选择全部可用维度。

从直接可视化的角度，以二维数据降维为例，PCA和LDA的区别如下图：

绿线：LDA，考虑了类内散度。

蓝线：PCA，不考虑类别，只关心降维后的整体方差最大。

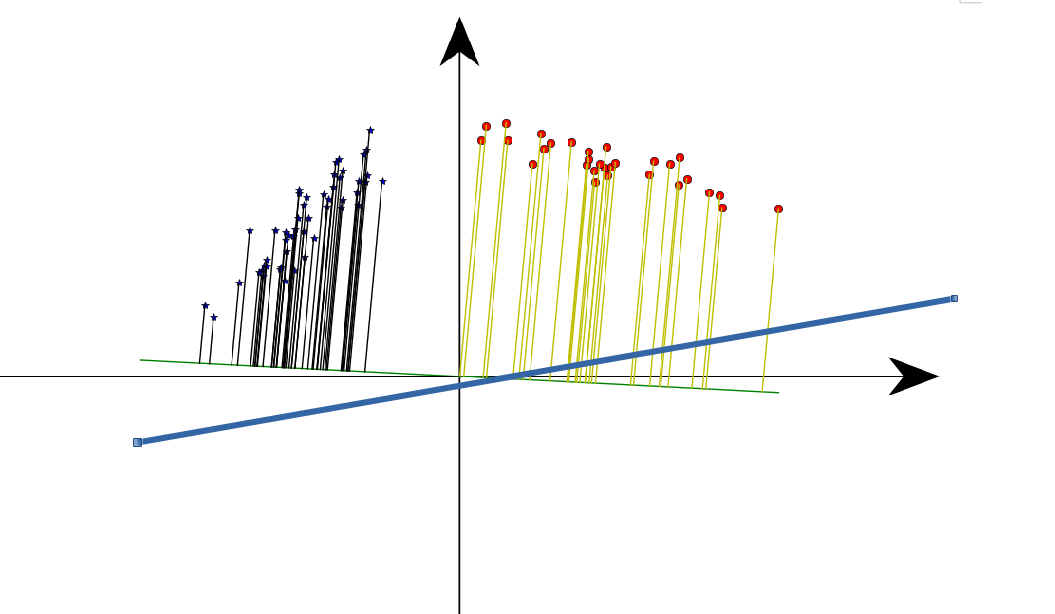
上图左侧是PCA的降维思想，它所作的只是将整组数据整体映射到最方便表示这组数据的坐标轴上，映射时没有利用任何数据内部的分类信息。因此，虽然PCA后的数据在表示上更加方便（降低了维数并能最大限度的保持原有信息），但在分类上也许会变得更加困难；上图右侧是LDA的降维思想，可以看到LDA充分利用了数据的分类信息，将两组数据映射到了另外一个坐标轴上，使得数据更易区分了（在低维上就可以区分，减少了运算量）。

线性判别分析LDA算法由于其简单有效性在多个领域都得到了广泛地应用，是目前机器学习、数据挖掘领域经典且热门的一个算法；但是算法本身仍然存在一些局限性：

- 当样本数量远小于样本的特征维数，样本与样本之间的距离变大使得距离度量失效，使LDA算法中的类内、类间离散度矩阵奇异，不能得到最优的投影方向，在人脸识别领域中表现得尤为突出
- LDA不适合对非高斯分布的样本进行降维
- LDA在样本分类信息依赖方差而不是均值时，效果不好
- LDA可能过度拟合数据

二、使用方法

为何降维

当特征选择完成后，可以直接训练模型了，但是可能由于特征矩阵过大，导致计算量大，训练时间长的问题，因此降低特征矩阵维度也是必不可少的。

常见的降维方法除了基于L1惩罚项的模型以外，另外还有主成分分析法（PCA）和线性判别分析（LDA），线性判别分析本身也是一个分类模型。

PCA和LDA有很多的相似点，其本质是要将原始的样本映射到维度更低的样本空间中，但是PCA和LDA的映射目标不一样：PCA是为了让映射后的样本具有最大的发散性；而LDA是为了让映射后的样本有最好的分类性能。

所以说PCA是一种无监督的降维方法，而LDA是一种有监督的降维方法。

4.1 主成分分析法（PCA）

使用decomposition库的PCA类选择特征的代码如下：

from sklearn.decomposition import PCA

#主成分分析法，返回降维后的数据

#参数n_components为主成分数目

PCA(n_components=2).fit_transform(iris.data)

4.2 线性判别分析法（LDA）

使用lda库的LDA类选择特征的代码如下：

from sklearn.lda import LDA

#线性判别分析法，返回降维后的数据

#参数n_components为降维后的维数

LDA(n_components=2).fit_transform(iris.data, iris.target)

三、引入了如下概念

类间散度，

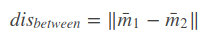
类内散度，

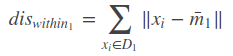
判别函数，

四、线性判别和二次判别

Ref: Quadratic Discriminant Analysis(QDA)

与线性判别分析类似，二次判别分析是另外一种线性判别分析算法，二者拥有类似的算法特征，区别仅在于：

- 当不同分类样本的协方差矩阵相同时，使用线性判别分析；
- 当不同分类样本的协方差矩阵不同时，则应该使用二次判别。

下图显示了在固定协方差矩阵以及不同协方差矩阵下LDA和QDA的表现差异：

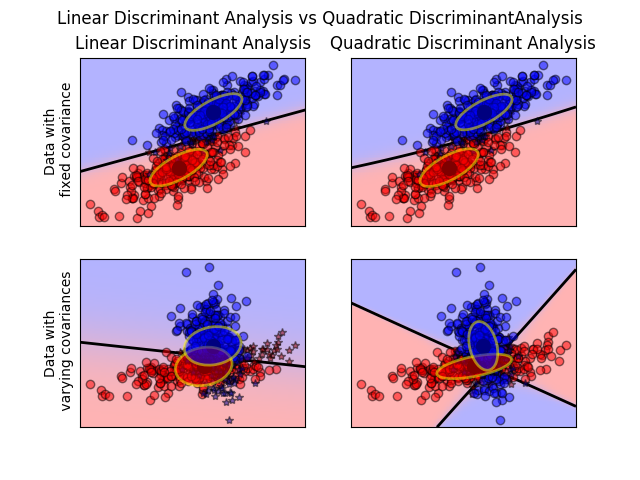
由图中可以看出，在固定协方差矩阵下，LDA和QDA是没有分类结果差异的（上面两张图）；
但在不同的协方差矩阵下，LDA和QDA的分类边界明显存在差异，而且LDA已经不能准确的划分数据（下面两张图）。

【怎么可能样本都是同样的协方差，感觉LDA没啥用处？】

print(__doc__)

from scipy import linalg

import numpy as np

import matplotlib.pyplot as plt

import matplotlib as mpl

from matplotlib import colors

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis

# #############################################################################

# Colormap

cmap = colors.LinearSegmentedColormap(

    'red_blue_classes',

    {'red': [(0, 1, 1), (1, 0.7, 0.7)],

     'green': [(0, 0.7, 0.7), (1, 0.7, 0.7)],

     'blue': [(0, 0.7, 0.7), (1, 1, 1)]})

plt.cm.register_cmap(cmap=cmap)

# #############################################################################

# Generate datasets

def dataset_fixed_cov():

    '''Generate 2 Gaussians samples with the same covariance matrix'''

    n, dim = 300, 2

    np.random.seed(0)

    C = np.array([[0., -0.23], [0.83, .23]])

    X = np.r_[np.dot(np.random.randn(n, dim), C),

              np.dot(np.random.randn(n, dim), C) + np.array([1, 1])]

    y = np.hstack((np.zeros(n), np.ones(n)))

    return X, y

def dataset_cov():

    '''Generate 2 Gaussians samples with different covariance matrices'''

    n, dim = 300, 2

    np.random.seed(0)

    C = np.array([[0., -1.], [2.5, .7]]) * 2.

    X = np.r_[np.dot(np.random.randn(n, dim), C),

              np.dot(np.random.randn(n, dim), C.T) + np.array([1, 4])]

    y = np.hstack((np.zeros(n), np.ones(n)))

    return X, y

# #############################################################################

# Plot functions

def plot_data(lda, X, y, y_pred, fig_index):

    splot = plt.subplot(2, 2, fig_index)

    if fig_index == 1:

        plt.title('Linear Discriminant Analysis')

        plt.ylabel('Data with\n fixed covariance')

    elif fig_index == 2:

        plt.title('Quadratic Discriminant Analysis')

    elif fig_index == 3:

        plt.ylabel('Data with\n varying covariances')

    tp = (y == y_pred)  # True Positive

    tp0, tp1 = tp[y == 0], tp[y == 1]

    X0, X1 = X[y == 0], X[y == 1]

    X0_tp, X0_fp = X0[tp0], X0[~tp0]

    X1_tp, X1_fp = X1[tp1], X1[~tp1]

    alpha = 0.5

    # class 0: dots

    plt.plot(X0_tp[:, 0], X0_tp[:, 1], 'o', alpha=alpha,

             color='red', markeredgecolor='k')

    plt.plot(X0_fp[:, 0], X0_fp[:, 1], '*', alpha=alpha,

             color='#990000', markeredgecolor='k')  # dark red

    # class 1: dots

    plt.plot(X1_tp[:, 0], X1_tp[:, 1], 'o', alpha=alpha,

             color='blue', markeredgecolor='k')

    plt.plot(X1_fp[:, 0], X1_fp[:, 1], '*', alpha=alpha,

             color='#000099', markeredgecolor='k')  # dark blue

    # class 0 and 1 : areas

    nx, ny = 200, 100

    x_min, x_max = plt.xlim()

    y_min, y_max = plt.ylim()

    xx, yy = np.meshgrid(np.linspace(x_min, x_max, nx),

                         np.linspace(y_min, y_max, ny))

    Z = lda.predict_proba(np.c_[xx.ravel(), yy.ravel()])

    Z = Z[:, 1].reshape(xx.shape)

    plt.pcolormesh(xx, yy, Z, cmap='red_blue_classes',

                   norm=colors.Normalize(0., 1.))

    plt.contour(xx, yy, Z, [0.5], linewidths=2., colors='k')

    # means

    plt.plot(lda.means_[0][0], lda.means_[0][1],

             'o', color='black', markersize=10, markeredgecolor='k')

    plt.plot(lda.means_[1][0], lda.means_[1][1],

             'o', color='black', markersize=10, markeredgecolor='k')

    return splot

def plot_ellipse(splot, mean, cov, color):

    v, w = linalg.eigh(cov)

    u = w[0] / linalg.norm(w[0])

    angle = np.arctan(u[1] / u[0])

    angle = 180 * angle / np.pi  # convert to degrees

    # filled Gaussian at 2 standard deviation

    ell = mpl.patches.Ellipse(mean, 2 * v[0] ** 0.5, 2 * v[1] ** 0.5,

                              180 + angle, facecolor=color,

                              edgecolor='yellow',

                              linewidth=2, zorder=2)

    ell.set_clip_box(splot.bbox)

    ell.set_alpha(0.5)

    splot.add_artist(ell)

    splot.set_xticks(())

    splot.set_yticks(())

def plot_lda_cov(lda, splot):

    plot_ellipse(splot, lda.means_[0], lda.covariance_, 'red')

    plot_ellipse(splot, lda.means_[1], lda.covariance_, 'blue')

def plot_qda_cov(qda, splot):

    plot_ellipse(splot, qda.means_[0], qda.covariances_[0], 'red')

    plot_ellipse(splot, qda.means_[1], qda.covariances_[1], 'blue')

for i, (X, y) in enumerate([dataset_fixed_cov(), dataset_cov()]):

    # Linear Discriminant Analysis

    lda = LinearDiscriminantAnalysis(solver="svd", store_covariance=True)

    y_pred = lda.fit(X, y).predict(X)

    splot = plot_data(lda, X, y, y_pred, fig_index=2 * i + 1)

    plot_lda_cov(lda, splot)

    plt.axis('tight')

    # Quadratic Discriminant Analysis

    qda = QuadraticDiscriminantAnalysis(store_covariances=True)

    y_pred = qda.fit(X, y).predict(X)

    splot = plot_data(qda, X, y, y_pred, fig_index=2 * i + 2)

    plot_qda_cov(qda, splot)

    plt.axis('tight')

plt.suptitle('Linear Discriminant Analysis vs Quadratic Discriminant'

             'Analysis')

plt.show()

End.