An overnight dance in discotheque

An overnight dance in discotheque

time limit per test 2 seconds

memory limit per test 256 megabytes

input standard input

output standard output

The crowdedness of the discotheque would never stop our friends from having fun, but a bit more spaciousness won't hurt, will it?

The discotheque can be seen as an infinite xy-plane, in which there are a total of n dancers. Once someone starts moving around, they will move only inside their own movement range, which is a circular area Ci described by a center (xi, yi) and a radius ri. No two ranges' borders have more than one common point, that is for every pair (i, j) (1 ≤ i < j ≤ n) either ranges Ci and Cj are disjoint, or one of them is a subset of the other. Note that it's possible that two ranges' borders share a single common point, but no two dancers have exactly the same ranges.

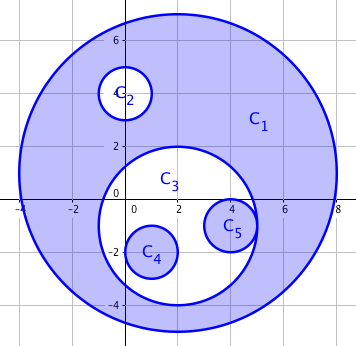
Tsukihi, being one of them, defines the spaciousness to be the area covered by an odd number of movement ranges of dancers who are moving. An example is shown below, with shaded regions representing the spaciousness if everyone moves at the same time.

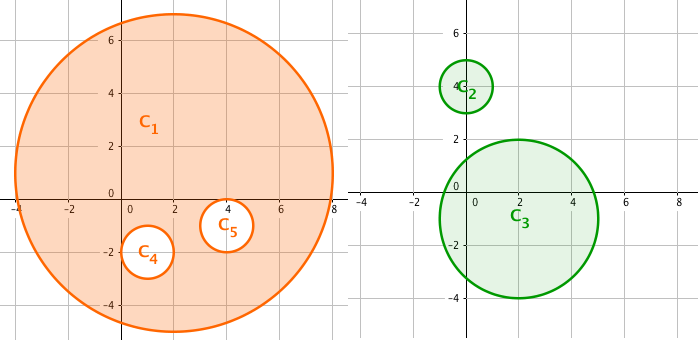
But no one keeps moving for the whole night after all, so the whole night's time is divided into two halves — before midnight and after midnight. Every dancer moves around in one half, while sitting down with friends in the other. The spaciousness of two halves are calculated separately and their sum should, of course, be as large as possible. The following figure shows an optimal solution to the example above.

By different plans of who dances in the first half and who does in the other, different sums of spaciousness over two halves are achieved. You are to find the largest achievable value of this sum.

Input

The first line of input contains a positive integer n (1 ≤ n ≤ 1 000) — the number of dancers.

The following n lines each describes a dancer: the i-th line among them contains three space-separated integers xi, yi and ri( - 106 ≤ xi, yi ≤ 106, 1 ≤ ri ≤ 106), describing a circular movement range centered at (xi, yi) with radius ri.

Output

Output one decimal number — the largest achievable sum of spaciousness over two halves of the night.

The output is considered correct if it has a relative or absolute error of at most 10 - 9. Formally, let your answer be a, and the jury's answer be b. Your answer is considered correct if .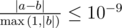

Examples

input

5
2 1 6
0 4 1
2 -1 3
1 -2 1
4 -1 1

output

138.23007676

input

8
0 0 1
0 0 2
0 0 3
0 0 4
0 0 5
0 0 6
0 0 7
0 0 8

output

289.02652413

Note

The first sample corresponds to the illustrations in the legend.

题解：

因为圆与圆之间只有两种关系，即相离和相包含，所以就可以根据是否相包含建立一棵树。

因为只有奇数部分才算宽敞度，所以自然就可以想到用0和1来表示在奇数层和偶数层。

又因为要将圆分成两个部分，综上所述，状态即为f[x][0/1][0/1]表示以x为根节点的树，x放在左边奇数层或偶数层和x放在右边奇数层或偶数层的最大值。

由于父子节点的层数相差一，所以从下到上动归的时候需要做一个异或运算。

代码如下：

#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<stack>
#include<ctime>
#include<vector>
#define pai (3.14159265358979323846)//像我这种辣鸡只会手打二十位的π
using namespace std;
int n,m;
int x[],y[],r[];
int father[];
long long f[][][];
struct node
{
    int next,to;
}edge[];
int head[],size=;
void putin(int from,int to)
{
    size++;
    edge[size].to=to;
    edge[size].next=head[from];
    head[from]=size;
}
bool judge(int a,int b)
{
    if((long long)(x[a]-x[b])*(x[a]-x[b])+(long long)(y[a]-y[b])*(y[a]-y[b])<=(long long)(r[a]-r[b])*(r[a]-r[b]))return ;
    else return ;
}
void dfs(int x,int fa)
{
    int i,j,k;
    long long g[][]={};
    for(i=head[x];i!=-;i=edge[i].next)
    {
        int y=edge[i].to;
        if(y!=fa)
        {
            dfs(y,x);
            for(j=;j<=;j++)
            {
                for(k=;k<=;k++)
                {
                    g[j][k]+=f[y][j][k];
                }
            }
        }
    }
    for(i=;i<=;i++)
    {
        for(j=;j<=;j++)
        {
            f[x][i][j]=max(g[i^][j]+(long long)r[x]*r[x]*(i==?():(-)),g[i][j^]+(long long)r[x]*r[x]*(j==?():(-)));
        }
    }
}
int main()
{
    int i,j;
    scanf("%d",&n);
    memset(head,-,sizeof(head));
    for(i=;i<=n;i++)
    {
        scanf("%d%d%d",&x[i],&y[i],&r[i]);
    }
    memset(father,-,sizeof(father));
    for(i=;i<=n;i++)
    {
        for(j=;j<=n;j++)
        {
            if(i!=j&&r[i]<=r[j]&&judge(i,j))
            {
                if(father[i]==-||r[father[i]]>r[j])father[i]=j;
            }
        }
        putin(father[i],i);
    }
    long long ans=;
    for(i=;i<=n;i++)
    {
        if(father[i]==-)
        {
            dfs(i,-);
            ans+=f[i][][];
        }
    }
    printf("%.8lf",ans*pai);
    return ;
}