2017中国大学生程序设计竞赛 - 网络选拔赛 HDU 6155 Subsequence Count 矩阵快速幂

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6155

题意：

题解来自：http://www.cnblogs.com/iRedBean/p/7398272.html

先考虑dp求01串的不同子序列的个数。

dp[i][j]表示用前i个字符组成的以j为结尾的01串个数。

如果第i个字符为0，则dp[i][0] = dp[i-1][1] + dp[i-1][0] + 1，dp[i][1] = dp[i-1][1]

如果第i个字符为1，则dp[i][1] = dp[i-1][1] + dp[i-1][0] + 1，dp[i][0] = dp[i-1][0]

显然这是线性递推，我们考虑如何用矩阵表示这种递推关系。

下面分别对应加入一个字符0或1时表示递推关系的矩阵。

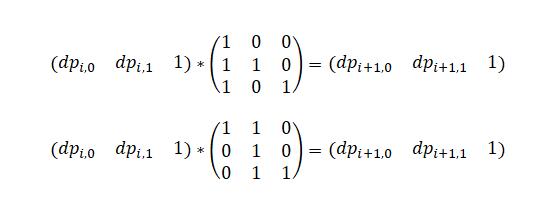
然后用线段树维护每个区间的矩阵乘积就可以解决查询操作了。

对于修改操作，我们给区间维护一个flip标记，表示该区间是否要翻转，用线段树区间更新的方法去更新flip标记就好了。

将一个区间翻转后，它对应矩阵也要发生改变，这里我们只要将矩阵的第一列与第二列交换后再将第一行与第二行交换就好了。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+6;
const int mod = 1e9+7;
typedef long long LL;
struct Matrix{
    LL maze[3][3];
    friend Matrix operator*(const Matrix& a, const Matrix& b){
        Matrix c;
        for(int i=0; i<3; i++){
            for(int j=0; j<3; j++){
                c.maze[i][j]=0;
                for(int k=0; k<3; k++){
                    c.maze[i][j]+=a.maze[i][k]*b.maze[k][j];
                    c.maze[i][j]%=mod;
                }
            }
        }
        return c;
    }
};
const Matrix m[2]={{1,0,0,1,1,0,1,0,1},{1,1,0,0,1,0,0,1,1}};
Matrix T[maxn<<2];
bool flip[maxn<<2];
char s[maxn];
void build(int l, int r, int rt){
    flip[rt] = 0;
    if(l == r){
        T[rt] = m[s[l]-'0'];
        return;
    }
    int mid = (l+r)>>1;
    build(l, mid, rt*2);
    build(mid+1, r, rt*2+1);
    T[rt] = T[rt*2]*T[rt*2+1];
}
void Flip(Matrix &mat){
    swap(mat.maze[0][0],mat.maze[0][1]);
    swap(mat.maze[1][0],mat.maze[1][1]);
    swap(mat.maze[2][0],mat.maze[2][1]);
    swap(mat.maze[0][0],mat.maze[1][0]);
    swap(mat.maze[0][1],mat.maze[1][1]);
    swap(mat.maze[0][2],mat.maze[1][2]);
}
void pushdown(int rt){
    if(flip[rt]){
        flip[rt*2]^=flip[rt];
        flip[rt*2+1]^=flip[rt];
        Flip(T[rt*2]);
        Flip(T[rt*2+1]);
        flip[rt]=false;
    }
}
void update(int L, int R, int l, int r, int rt){
    if(L<=l&&r<=R){
        flip[rt]^=1;
        Flip(T[rt]);
        return;
    }
    pushdown(rt);
    int mid=(l+r)/2;
    if(R<=mid) update(L,R,l,mid,rt*2);
    else if(L>mid) update(L,R,mid+1,r,rt*2+1);
    else{
        update(L,mid,l,mid,rt*2);
        update(mid+1,R,mid+1,r,rt*2+1);
    }
    T[rt]=T[rt*2]*T[rt*2+1];
}
Matrix query(int L, int R, int l, int r, int rt){
    if(L<=l&&r<=R){
        return T[rt];
    }
    pushdown(rt);
    int mid=(l+r)/2;
    if(R<=mid) return query(L,R,l,mid,rt*2);
    else if(L>mid) return query(L,R,mid+1,r,rt*2+1);
    else return query(L,mid,l,mid,rt*2)*query(mid+1,R,mid+1,r,rt*2+1);
}
int main()
{
    int T,n,q;
    scanf("%d", &T);
    while(T--)
    {
        scanf("%d%d",&n,&q);
        scanf("%s",s+1);
        build(1,n,1);
        while(q--)
        {
            int op,l,r;
            scanf("%d%d%d",&op,&l,&r);
            if(op==1) update(l,r,1,n,1);
            else{
                Matrix ret = query(l,r,1,n,1);
                printf("%lld\n", (ret.maze[2][0]+ret.maze[2][1])%mod);
            }
        }
    }
    return 0;
}