noip提高组2011 Mayan游戏

Mayan游戏

描述

Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个7行5列的棋盘，上面堆放着一些方块，方块不能悬空堆放，即方块必须放在最下面一行，或者放在其他方块之上。**游戏通关是指在规定的步数内消除所有的方块，**消除方块的规则如下：

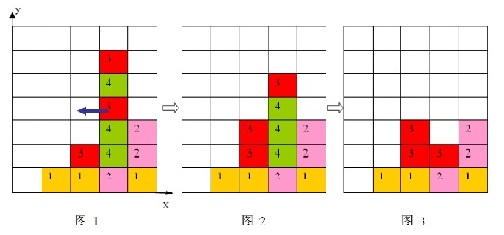
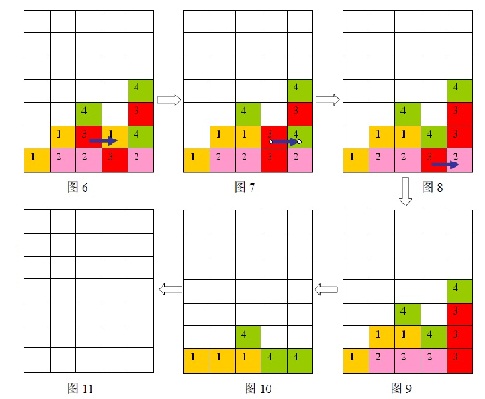
1、每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格：当拖动这一方块时，如果拖动后到达的位置（以下称目标位置）也有方块，那么这两个方块将交换位置（参见图6到图7）；如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落（直到不悬空，参见图1和图2)；

2、任一时刻，如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除（参见图1到图3）。

注意：
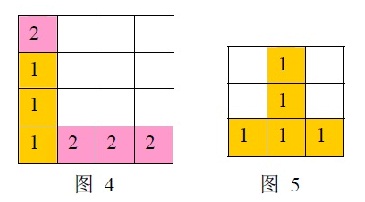
a) 如果同时有多组方块满足消除条件，几组方块会同时被消除（例如下面图4，三个颜色为1的方块和三个颜色为2的方块会同时被消除，最后剩下一个颜色为2的方块）。

b) 当出现行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除（例如下面图5所示的情形，5个方块会同时被消除）。

3、方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除。注意：掉落的过程中将不会有方块的消除。

上面图1到图3给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为（0, 0），将位于（3, 3）的方块向左移动之后，游戏界面从图1变成图2所示的状态，此时在一竖列上有连续三块颜色为4的方块，满足消除条件，消除连续3块颜色为4的方块后，上方的颜色为3的方块掉落，形成图3所示的局面。

格式

输入格式

第一行为一个正整数n，表示要求游戏关的步数。

接下来的5行，描述7*5的游戏界面。每行若干个整数，每两个整数之间用一个空格隔开，每行以一个0 结束，自下向上表示每竖列方块的颜色编号（颜色不多于10种，从1开始顺序编号，相同数字表示相同颜色）。

输入数据保证初始棋盘中没有可以消除的方块。

输出格式

如果有解决方案，输出n行，每行包含3个整数x，y，g，表示一次移动，每两个整数之间用一个空格隔开，其中（x，y）表示要移动的方块的坐标，g表示移动的方向，1表示向右移动，-1表示向左移动。**注意：多组解时，按照x为第一关键字，y为第二关键字，1优先于-1，给出一组字典序最小的解。游戏界面左下角的坐标为(0, 0)。**
如果没有解决方案，输出一行，包含一个整数-1。

样例1

样例输入1

3
1 0
2 1 0
2 3 4 0
3 1 0
2 4 3 4 0

样例输出1

2 1 1
3 1 1
3 0 1

限制

3s

提示

样例输入的游戏局面如图6到图11所示。依次移动的三步是：（2，1）处的方格向右移动，（3，1）处的方格向右移动，（3，0）处的方格向右移动，最后可以将棋盘上所有方块消除。

数据规模如下：
对于30%的数据，初始棋盘上的方块都在棋盘的最下面一行；
对于100%的数据，0 < n ≤ 5。

这题主要难点不在搜索，而在如何消除联通的块和让快掉落，搜索还是挺好写的，还可以在搜的时候加个剪枝：若有一种颜色块只有一或两块，直接return

#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
using std :: swap;
int s[6][8],n;
struct T {
  int x,y,z;
}ans[6];
inline bool check(int tmp[6][8]) {
  bool pd[6][8],flag = false;
  memset(pd,false,sizeof(pd));
  for (int i = 0;i <= 5;i++)
    for (int j = 0;j <= 7;j++)
      if (tmp[i][j]) {
        if (i <= 3 && tmp[i][j] == tmp[i+1][j] && tmp[i+1][j] == tmp[i+2][j]) pd[i][j] = pd[i+1][j] = pd[i+2][j] = true;  //标记起来相同的（列）
        if (j <= 5 && tmp[i][j] == tmp[i][j+1] && tmp[i][j+1] == tmp[i][j+2]) pd[i][j] = pd[i][j+1] = pd[i][j+2] = true;  //标记起来相同的（行）
      }
  for (int i = 0;i < 5;i++)
    for (int j = 0;j < 7;j++)
      if (pd[i][j]) {
        tmp[i][j] = 0;  //消掉
        flag = true;
      }
  return flag;
}
inline void down(int tmp[6][8]) {
  for (int i = 0;i < 5;i++) {
    int t = 0;
    for(int j = 0;j < 7;j++) {
      int l = tmp[i][j];
      tmp[i][j] = 0;
      if (l) tmp[i][t++] = l;  //掉落
    }
  }
}
void dfs(int tot,int map[6][8]) {
  if (tot == n) {
    bool flag = true;
    for (int i = 0;i < 5;i++)
      for (int j = 0;j < 7;j++)
        if (map[i][j]) {
          flag = false;
          break;
        }
    if (flag) {  //是否消完
      for (int i = 1;i <= n;i++) printf("%d %d %d\n",ans[i].x,ans[i].y,ans[i].z);
      exit(false);
    }
    return;
  }
  int cnt[11];
  memset(cnt,0,sizeof(cnt));
  for (int i = 0;i < 5;i++)
    for (int j = 0;j < 7;j++) cnt[map[i][j]]++;  //统计每种颜色有多少块
  for (int i = 1;i <= 10;i++)
    if (cnt[i] == 1 || cnt[i] == 2) return;  //若不足三块，直接return
  for (int i = 0;i < 4;i++)
    for (int j = 0;j < 7;j++)
      if (map[i][j] != map[i+1][j]) {  //把不一样的两个相邻块交换
        int tmp[6][8];
        memcpy(tmp,map,sizeof(tmp));
        if (tmp[i][j]) {
          ans[tot+1].x = i;
          ans[tot+1].y = j;
          ans[tot+1].z = 1;
        } else {
          ans[tot+1].x = i+1;
          ans[tot+1].y = j;
          ans[tot+1].z = -1;
        }
        swap(tmp[i][j],tmp[i+1][j]);  //交换
        down(tmp);  //掉落
        while (check(tmp)) down(tmp);  //消掉，然后掉落
        dfs(tot+1,tmp);  //下一步
      }
}
int main() {
  freopen("mayan.in","r",stdin);
  freopen("mayan.out","w",stdout);
  scanf("%d",&n);
  for (int i = 0;i < 5;i++) {  //读入
    int x,t = 0;
    read : scanf("%d",&x);
    if (x) {
      s[i][t++] = x;
      goto read;
    }
  }
  dfs(0,s);
  printf("-1");  //无解输出-1
  return 0;
}