[CodeForces - 1225C]p-binary 【数论】【二进制】

[CodeForces - 1225C]p-binary 【数论】【二进制】

标签： 题解 codeforces题解 数论

---

题目描述

Time limit

2000 ms

Memory limit

524288 kB

Source

Technocup 2020 - Elimination Round 2

Tags

bitmasks brute force math *1600

Site

https://codeforces.com/problemset/problem/1225/c

题面

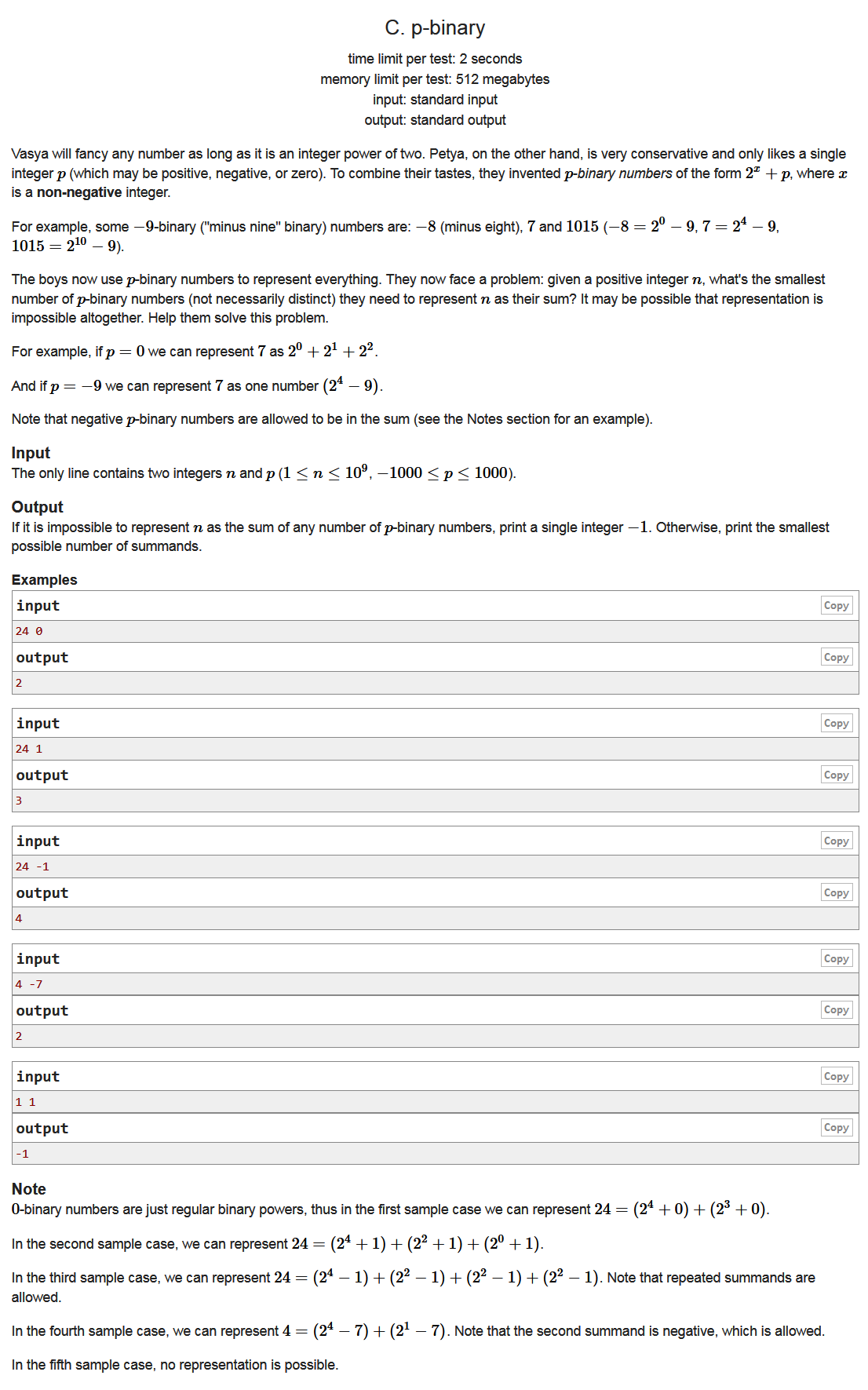
Example

Input1

24 0

Output1

2

Input2

24 1

Output2

3

Input3

24 -1

Output3

4

Input4

4 -7

Output4

2

Input5

1 1

Output5

-1

题目大意

给定\(n, p\)，使\(n\)能表达成这样的形式\(n = \sum_{i = 1}^{m}(2^{a[i]} + p)\)（\(a[i] = 0,1,2,3, \dots\)）。问最小的\(m\)是多少？如果无法写成上述表达，则输出-1。

例如，

给定\(n = 24, k = 1\)，\(24 = （2^4 + 1） + （2^2 + 1）+ （2^0 + 1）\)。这样\(m\)最小为3。

---

解析

可将上式变形，\(n - m \times p = \sum_{i = 1}^{m}2^{a[i]}\)。

令\(d(x)\)表示\(x\)的二进制形式中\(1\)的个数。

我们不难发现，满足\(d(n - m \times p) \leq m \leq n - m \times p\)，即有\(n - m \times p = \sum_{i = 1}^{m}2^{a[i]}\)。

因为\(2^i = 2^{i - 1} + 2 ^ {i - 1}\)，所以\(m\)可以大于这个数的二进制中\(1\)的个数。

而\(2^0 = 1\)的时候就无法再往下分了，所以\(m\)要小于等于这个数的本身。

这样我们就可以通过简单枚举\(m\)得出答案。

为什么m可以通过枚举得出？m不会很大吗？

\(n - m \times p = \sum_{i = 1}^{m}2^{a[i]}\)等式左边是线性增长，等式右边是指数增长。能使等号成立的\(m\)不会很大。

---

通过代码

/*
Status
	Accepted
Time
	31ms
Memory
	8kB
Length
	584
Lang
	GNU G++11 5.1.0
Submitted
	2019-12-20 09:17:54

RemoteRunId
	67258530
*/

#include <bits/stdc++.h>
#define lowbit(i) i & -i                //一个数的二进制表示中，1的最低位.
using namespace std;

const int INF = 1e5;
int n, p;

int binary_digit(int x)            //找到一个数的二进制表示中，有几个1.
{
    int cnt = 0;

    while(x){
        x -= lowbit(x);
        cnt ++;
    }

    return cnt;
}
void work()
{
    for(int i = 1; i < INF; i ++){      //枚举.
        if(n - i * p < 0){              //n>0，出现小于0的情况就直接结束.
            puts("-1");
            return;
        }

        if(binary_digit(n - i * p) <= i && i <= n - i * p){    //落在这个区间的就能满足等式.
            printf("%d", i);
            return;
        }
    }

    puts("-1");
    return;
}
int main()
{
    scanf("%d%d", &n, &p);

    work();

    return 0;
}

---