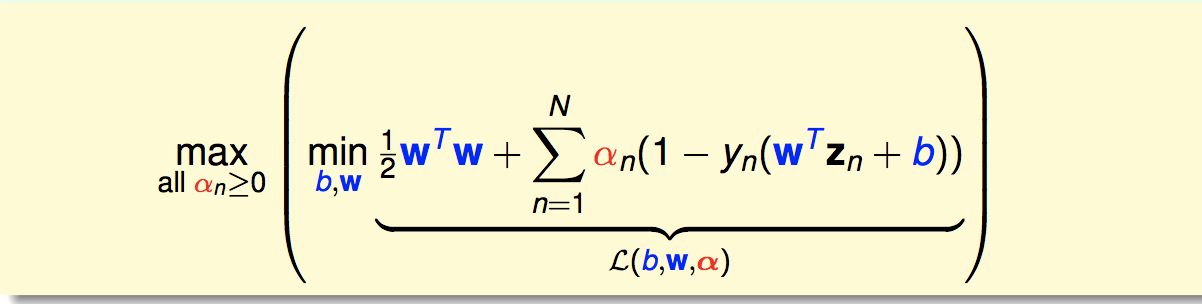《机器学习技法》---对偶SVM
1.对偶问题的推导
为什么要求解对偶问题?一是对偶问题往往更容易求解,二是可以自然的引入核函数。
1.1 用拉格朗日函数将原问题转化为“无约束”等价问题
原问题是:

写出它的拉格朗日函数:

然后我们的原问题就等价为:

为什么可以这样等价:

即:对于不满足约束条件的(b,w),min里面趋于无穷大,因此min就把这些b,w舍去了;对于满足约束条件的解,min里面就刚好是原来的目标函数,刚好与原问题等价。
1.2 导出拉格朗日对偶问题
首先我们有如下成立:

然后我们取右边式子中的“best”阿尔法,仍然会有大于等于号成立,因为best is one of any:

这时右边的式子就是对偶问题。这里直接给出一个定理,当满足下面条件时(对于SVM来说刚好满足),原始问题和对偶问题的解是相同的:

并且它们的最优解满足KKT条件:偏导为0,对偶互补,拉格朗日乘子大于0.
1.3 用KKT条件来简化对偶问题
我们的对偶问题现在是:
根据KKT条件,我们有:

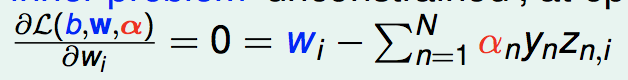
把第一个代进来:

再把第二个代进来:

这时候,我们的问题里面就只剩一个参数阿尔法了。再把平方项展开,写的好看一点,就得到了标准的硬间隔SVM对偶问题:

2. 解对偶问题
还是解QP那一套:

之后再求W和b:
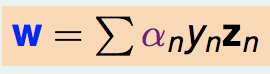 (所有支持向量的加权和)
(所有支持向量的加权和)
 (任取一个支持向量算出)
(任取一个支持向量算出)
3. 支持向量
引出对偶问题后,我们重现定义支持向量为阿尔法大于0的向量。他们一定是在边界上的(统计学习方法p107),但是在边界上的不一定阿尔法大于0:

前面我们也提到过,w和b的计算只需要支持向量,其他向量都是无用的:

《机器学习技法》---对偶SVM的更多相关文章
- 对偶SVM
1.对偶问题的推导 为什么要求解对偶问题?一是对偶问题往往更容易求解,二是可以自然的引入核函数. 1.1 用拉格朗日函数将原问题转化为"无约束"等价问题 原问题是: 写出它的拉格朗 ...
- SVM原理与实践
SVM迅速发展和完善,在解决小样本.非线性及高维模式识别问题中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中.从此迅速的发展起来,已经在许多领域(生物信息学,文本和手写识别等)都取 ...
- SVM1 线性SVM
一.Linear Support Vector Machine 接下来的讨论假设数据都是线性可分的. 1.1 SVM的引入:增大对测量误差的容忍度 假设有训练数据和分类曲线如下图所示: 很明显,三个分 ...
- SVM学习笔记
一.SVM概述 支持向量机(support vector machine)是一系列的监督学习算法,能用于分类.回归分析.原本的SVM是个二分类算法,通过引入“OVO”或者“OVR”可以扩展到多分类问题 ...
- SVM对偶形式
dual svm 对偶SVM linear SVM 可以用二次规划方法解 xn通过非线性转换变成zn SVM配合非线性特征转换 透过large-margin降低模型复杂度 透过特征转换得到弯弯曲曲的边 ...
- SVM笔记
1.前言 SVM(Support Vector Machine)是一种寻求最大分类间隔的机器学习方法,广泛应用于各个领域,许多人把SVM当做首选方法,它也被称之为最优分类器,这是为什么呢?这篇文章将系 ...
- 【机器学习算法基础+实战系列】SVM
概述 支持向量机是一种二分类模型,间隔最大使它有别于感知机.支持向量机学习方法由简至繁的模型:线性可分支持向量机(linear support vector machine in linearly s ...
- SVM小白教程(2):拉格朗日对偶
在上一篇文章中,我们推导出了 SVM 的目标函数: \[ \underset{(\mathbf{w},b)}{\operatorname{min}} ||\mathbf{w}|| \\ \operat ...
- SVM系列之拉格朗日对偶
在学习SVM(Support Vector Machine) 支持向量机时,对于线性可分的分类样本求出的分类函数为: 其中,分类超平面可以表示为:
随机推荐
- Java实现LRU算法
一.LRU算法简介 LRU(Least Recently Used)最近最久未使用算法 常见应用场景:内存管理中的页面置换算法.缓存淘汰中的淘汰策略等 二.实现理论 底层结构:双向链表 + HashM ...
- Java 内存映射文件
import java.io.*; import java.nio.MappedByteBuffer; import java.nio.channels.FileChannel; import jav ...
- 个人永久性免费-Excel催化剂功能第31波-数量金额分组凑数功能,财务表哥表姐最爱
在财务工作过程中,很大时候需要使用到凑数的需求,花了两三天时间认真研究了一下,本人水平也只能做代码搬运工,在用户体验上作了一下完善.完成了Excel版的凑数功能. 文章出处说明 原文在简书上发表,再同 ...
- 一个测试文件与源文件位于不同模块时Jacoco覆盖率配置的例子
问题描述: 我们有个多模块项目,由于种种原因(更常见的可能是需要集成测试)测试文件和源文件不在一个模块,Jacoco的覆盖率无法正确显示,查询了一些资料,发现中文的例子比较少,就把我自己的Demo贴一 ...
- 【ML入门】李宏毅机器学习笔记01-Learning Map
版权声明:小博主水平有限,希望大家多多指导.本文仅代表作者本人观点,转载请联系知乎原作者——BG大龍. 目录 1 什么是机器学习? 2 机器学习的3个步骤 3 李宏毅老师的机器学习课程 4 按“模型的 ...
- Linux系统安装Tomcat——.tar.gz版(old)
这里简单地阐述一下rpm.deb.tar.gz的区别. rpm格式的软件包适用于基于Red Hat发行版的系统,如Red Hat Linux.SUSE.Fedora. deb格式的软件包则是适用于基于 ...
- lr录制选项设置代理
解决录制时浏览器打不开录制时录不到脚本等浏览器兼容问题一.lr录制选项设置代理1.点击Options 2.点击Port Mapping→Newentrv 3.lr代理设置 ·Socket Servic ...
- RabbitMQ(三):RabbitMQ与Spring Boot简单整合
RabbitMQ是目前非常热门的一款消息中间件,不管是互联网大厂还是中小企业都在大量使用.Spring Boot的兴起,极大地简化了Spring的开发,本文将使用Spring Boot与RabbitM ...
- Java oop 多态
1.多态指对象的多种形态:引用多态与方法多态 注意: A:继承是多态的实现基础 B:方法重写也是多态的体现 2.引用多态 A:父类的引用可以指向本类的对象:父类 对象名 = new 父类( ...
- Django安装 测试、导入项目以及运行开发服务器
安装Django 下载Django包,解压缩. CMD 进入解压路径下. 执行:python setup.py install 增加环境变量: C:\Python27\Scripts 测试djang ...