100天搞定机器学习|Day 30-32 微积分的本质

3blue1brown系列课程，精美的动画，配上生动的讲解，非常适合帮助建立数学的形象思维，非常值得反复观看：

http://www.3blue1brown.com/

哔哩哔哩：

https://space.bilibili.com/88461692

作者还把制作视频的用到的代码放到了 github 上，有兴趣的同学可以研究看看

Github: https://github.com/3b1b/manim

我们节选其中一部分内容，领略一下微积分的奥妙

要了解微积分的本质，我们从一个大家都知道的公式说起。这个公式就是求圆的面积公式：A=πr²

 我们将用微积分的方式来推导这个公式，在这个过程中，我们将利用到微分，积分，和两者的互逆。

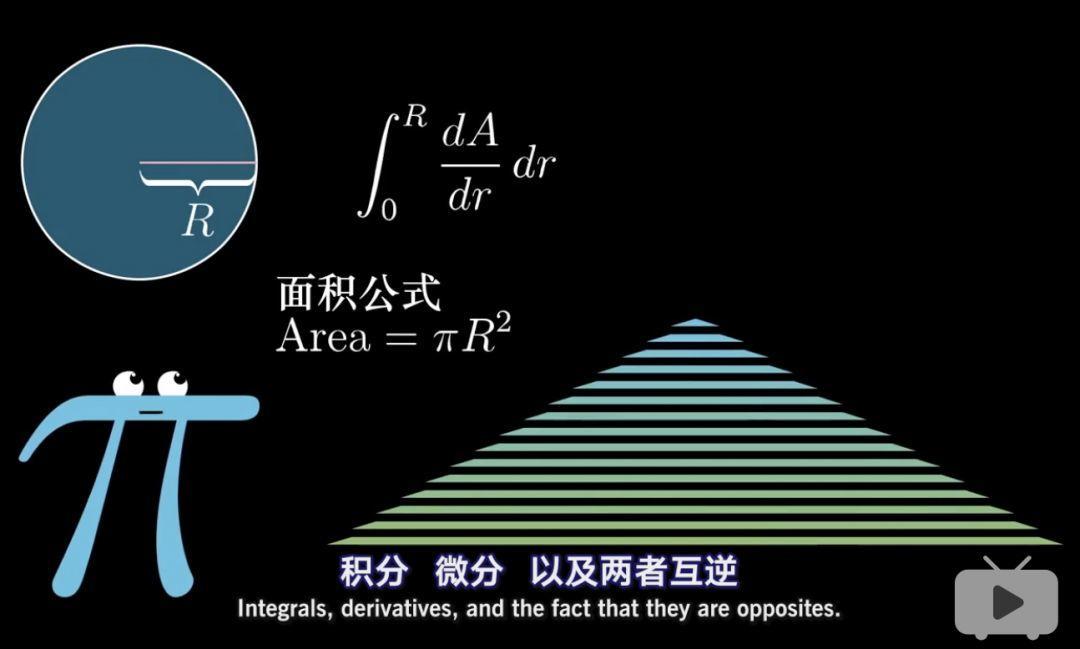
首先我们先将一个圆如下图切分成数个圆环。我们获得每个圆环的面积，然后将他们相加不就得到圆的面积了。

所以我们以相同的距离dr将圆切分成若干个同心圆环。

比如圆环的半径是3，dr取0.1 那么我们就将一个圆换分成了30个宽度都是0.1的同心圆环：

每一个圆环拉直会得到一个新的形状，我们将这个形状近似看做一个矩形

那么这个矩形的面积就是这个圆环的周长乘以dr，圆环的周长为圆环到圆心的距离*2π

那么每个圆环的近似面积面积就为：**2πr*dr**(这里的r是每个圆环到圆心的距离)

你会发现我们的dr 取值越小，那么我们计算出来的圆的面积也就越精确。

现在如果我们把所有近似矩从小到大一个接一个的排列在一起，我们会有一些全新的发现：

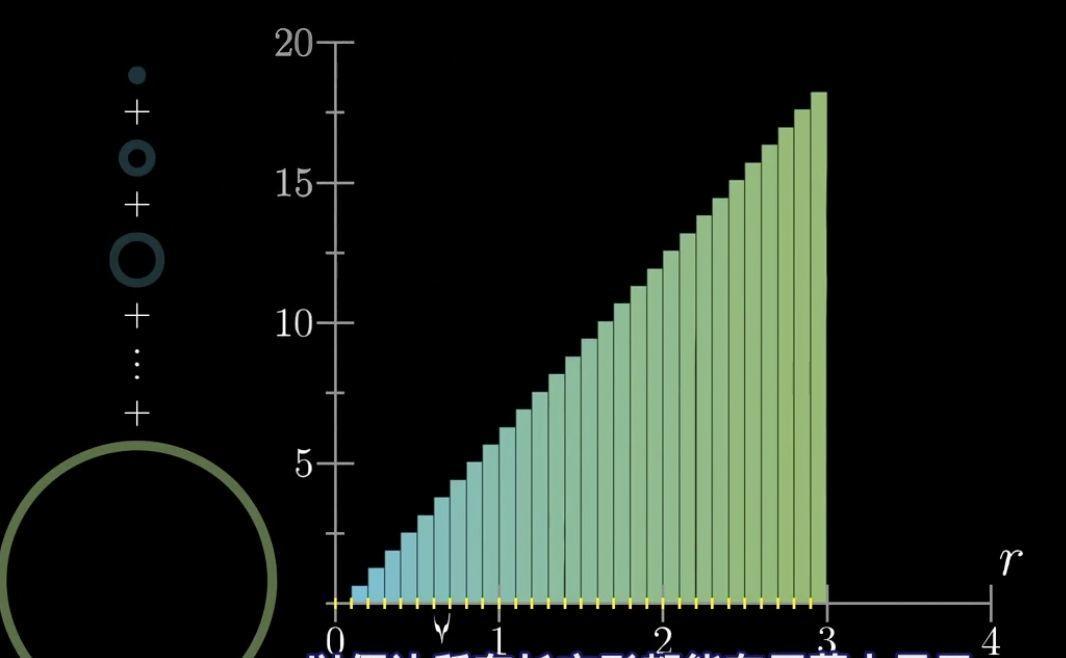
注意，为了方便观察我们y轴与x轴的比例为5：1

现在我们去的dr是0.1，而我们取的dr值越小，获得的圆环的数量就越多，而这些圆环的近似矩形面积相加起来的面积就靠近原来的圆的面积。

若是无限多个圆环，那么我们获得的近似值越来越靠近真实值。

可是我们取的圆环越多，那么计算量不就越大，无限多的就代表根本没法计算。

但注意，当dr取值无限小的时候，我们将所有圆环的面积加起来与下图三角形的面积是相同的。

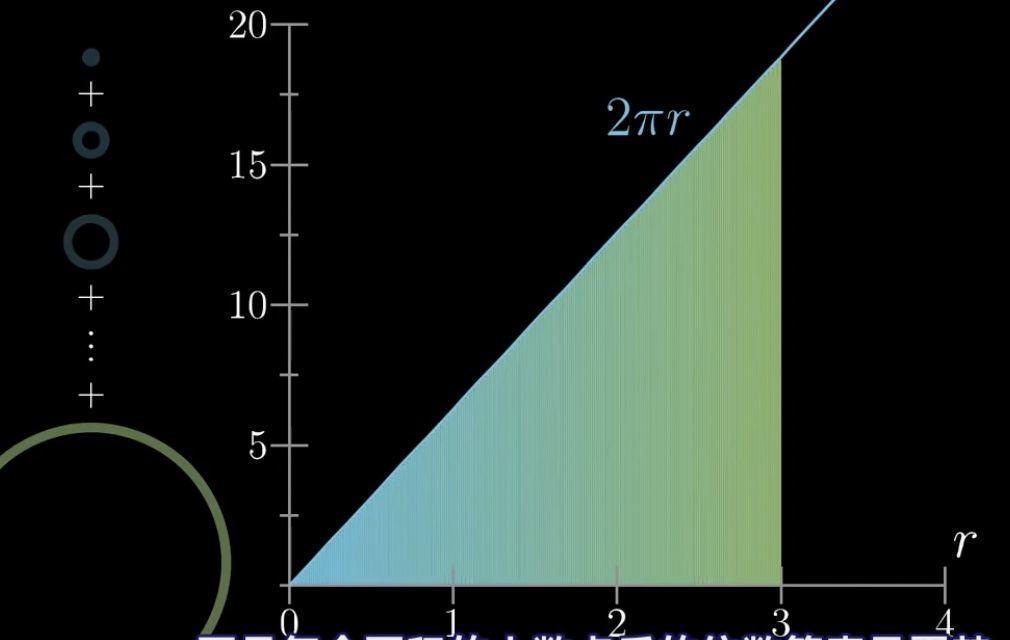
这个三角形的底是3 而高最大圆环的周长，也就是圆的周长：2π*3

如果圆的半径是r，那么它对应的三角形就是一个底为r，高为2π*r的三角形。根据三角形面积公式，我们得到

圆的面积为：πr²

对于数学家来说，你不光要找到答案，你还想要能发展处解决一般问题的工具和技巧

我们回想一下刚刚发生了什么。为什么这样做是可行的。这个从近似值到精确值的过程，通过这个过程，我们可以了解微积分的本质。

最开我们将问题化解为许多微小值的和，来获得一个近似的结果。

首先我们取每间隔dr值，取一个圆环。我们将一个圆换分成若干个小圆环，将其近似看成若干个矩形，我们就能获得近似的圆形面积。

这里的dr 不仅是圆环的宽度，也是每个圆环半径的间距。

我们将这个这个dr越缩小，dr值取的越小，所有矩形相加的面积就越接近于一个三角形的面积。

我们可以得出结论，原来的原型的面积恰好就是这个三角形的面积。

注意此时已经不是近似值，而是完全准确。

通过这种方法，我们重新推导了计算圆的面积的公式。

现在我们看看这种方法在其他的地方如何发挥作用。

例如，已知骑车在每个时间点上的速度，求这段时间骑车走了多远的距离。

我们可以用每个时间点的速度乘以这段微小的时间，然后相加求和，就是这一整段时间走的距离的近似值。

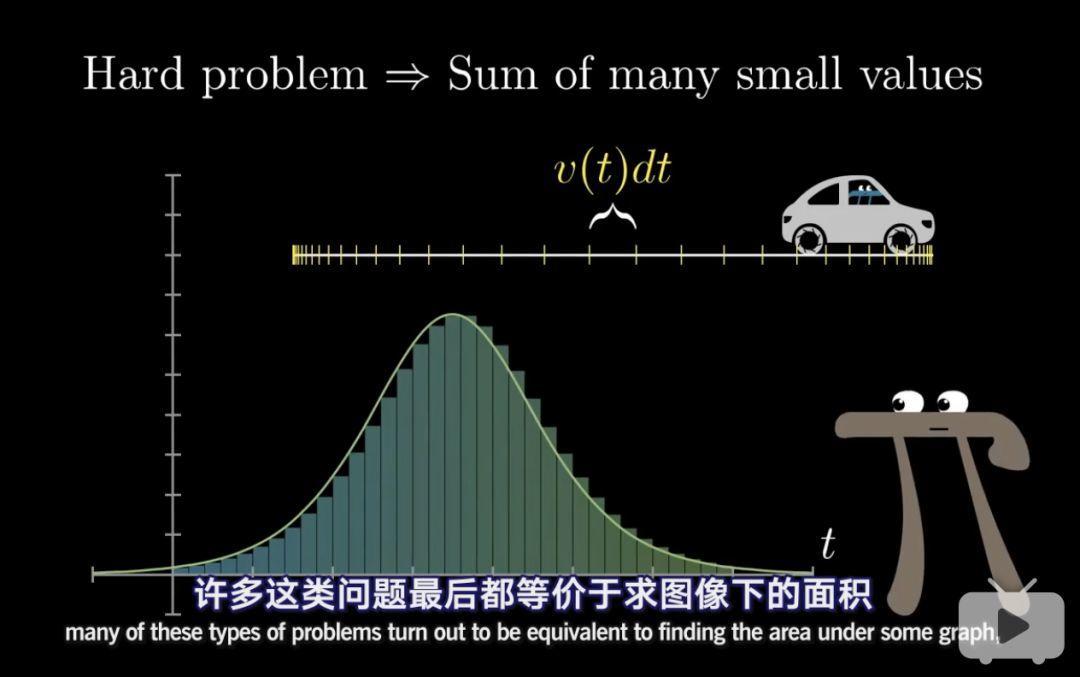
从图中，我们可以看出，最后我们将一个物理学的问题，变成了几何学的问题。这是不是很有趣？

还有很多的问题都可以这样来计算，我们将一个复杂的问题，拆解为若干近似于a*b然后相加求和的问题(如上面的速度乘以时间)，

其中每一个乘法计算中的a都是相同的。（如上一例子中，每一个时间点之间的距离是相同的，也就是vt中的t是相同的）

那么我们就可以将问题转化为若干细长的矩形面积(a*b不就是求矩形面积的公式？)相加取得近似值的问题。

若是我们取的a（在这个汽车例子中的t）取值越小，我们最终获得的值就越精确，而且越发靠近求下图面积的问题的。

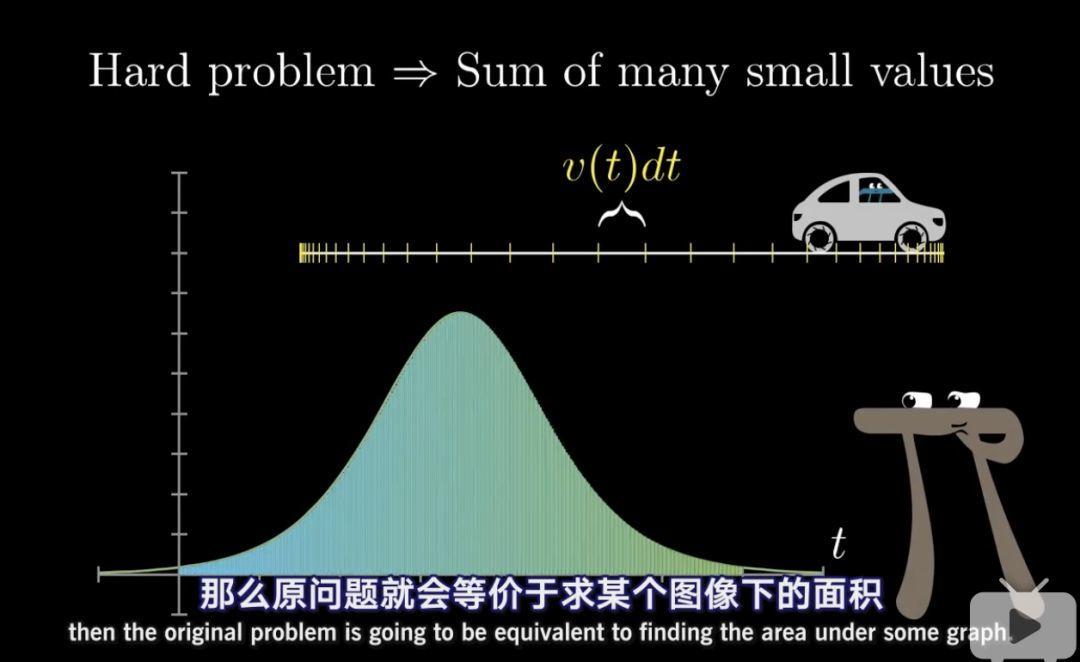
等等，这个形状的面积似乎也不是那么好求得。

似乎我们不会像求圆的面积的时候那么的幸运，得到图形正好是一个三角形。

如上题我们求一个汽车从发动到停止这段时间经过的距离，最后我们得到的这样一个形状，我们要怎么求它的面积呢？

一个二次函数的曲线下的面积要怎么求呢？

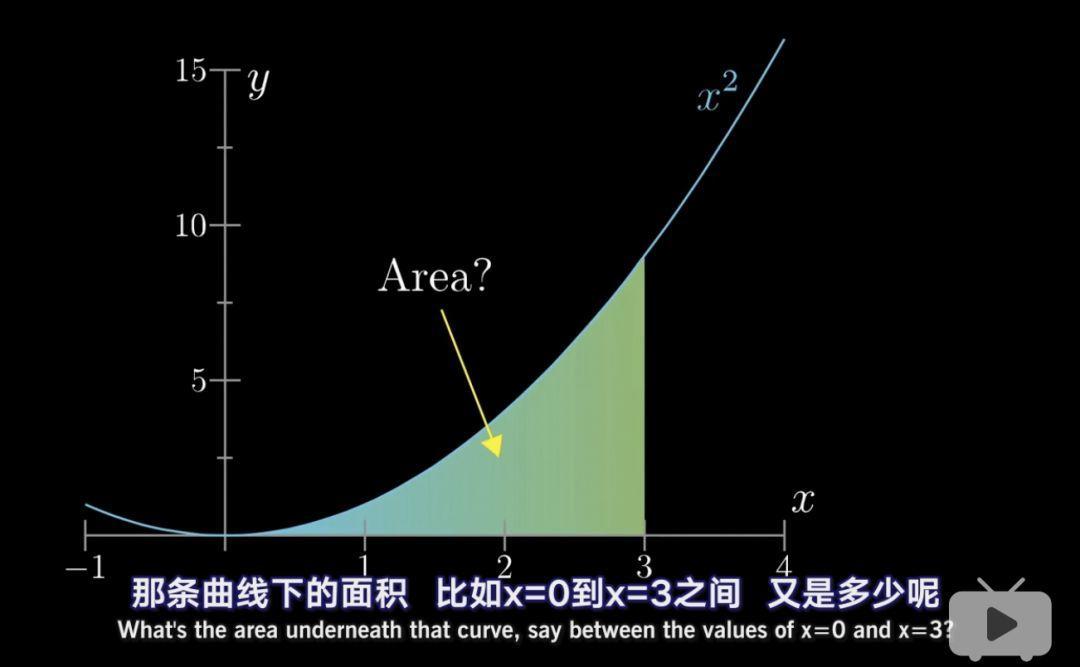
视频告诉我们，当你在数学上遇到一个特别难解的问题是，不要想着正面硬解，这样你往往会撞上南墙。

相反，你应该带着不明确的目的不断把玩这些概念。

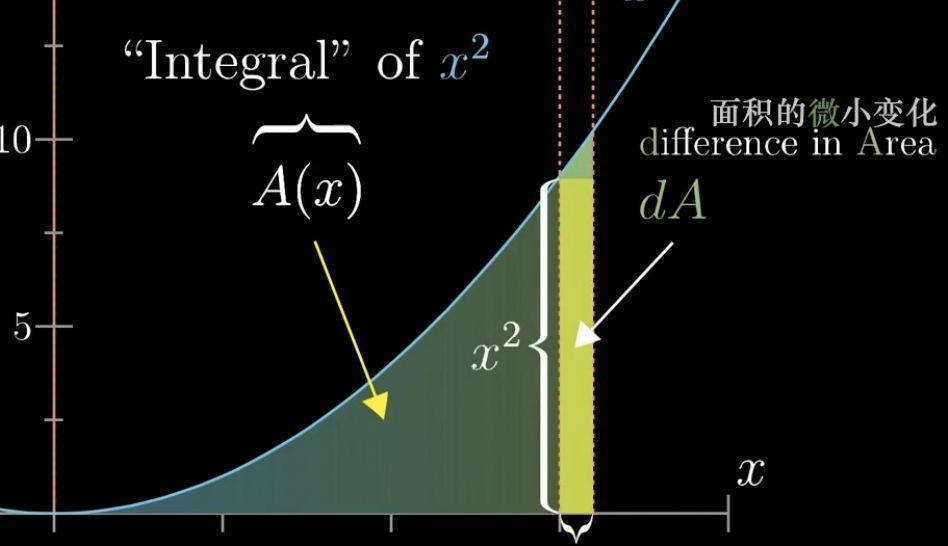
我们将二次函数，x²函数曲线下的面积设置A(x)

那么A(x)与x²之间有什么特殊关系呢？

如果我们将x的值增加一点点，那A(x²)的值回发生怎样的变化呢？

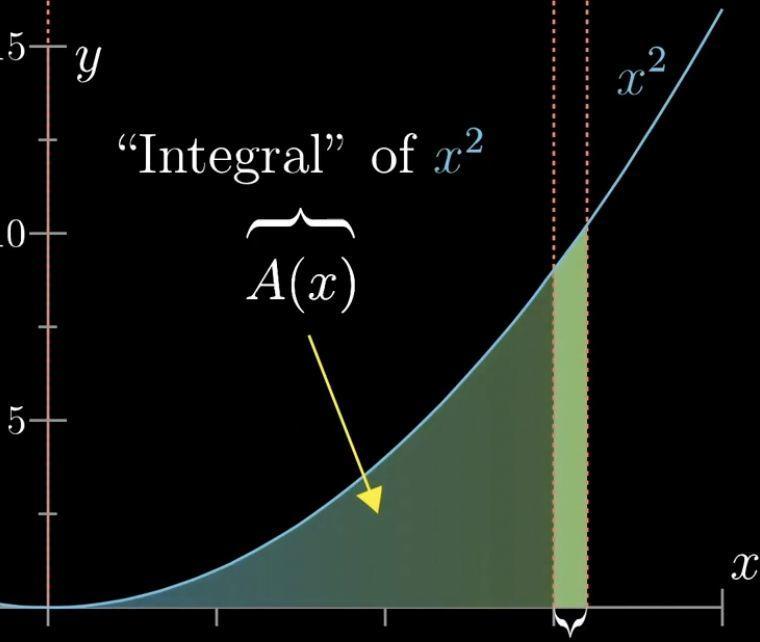
我们把增加的面积叫做dA，x的增加值叫做dx

我们将这个增加的面积近似看做一个矩形。

我们可以得到：

dA≈x²*dx   由此我们得到： dA/dx≈x²

这里我们dx的值取的越小，那么这个dA的面积就越接近矩形的面积。dA/dx也就越接近x²

我们将x=3,dx0.001代入这个公式可以得到

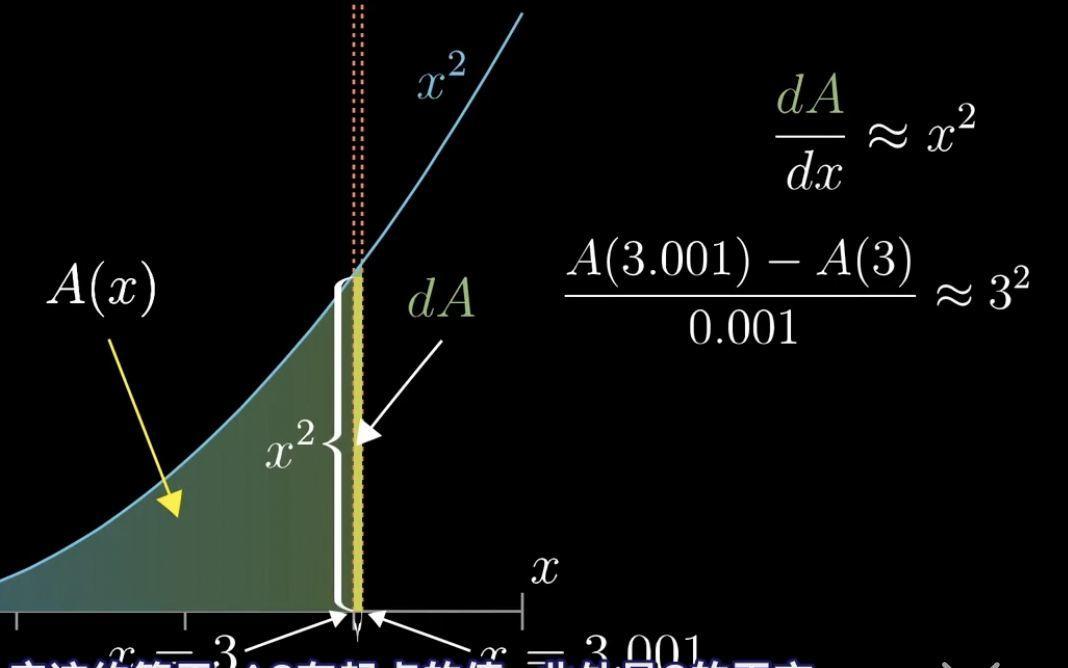
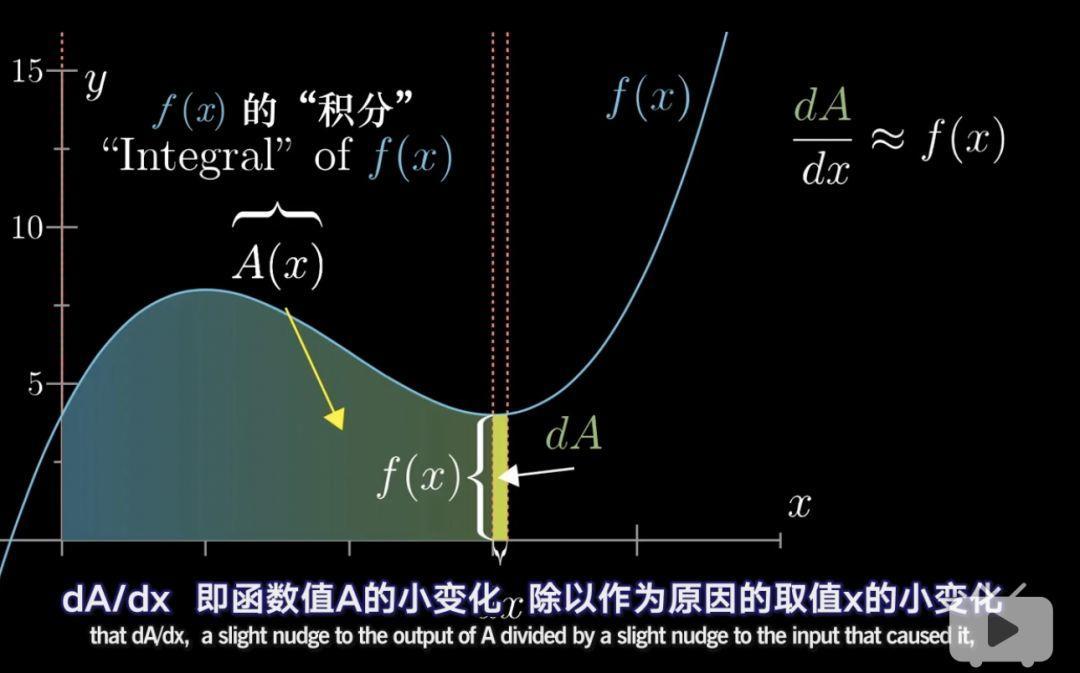
现在我们还是不知道神秘的A(x)，但是我们有了这样一个一个公式：dA/dx≈f(x)

dx取值越小，这个公式就越精确。

作者：guolaomao@cnblogs

https://www.cnblogs.com/guolaomao/category/1136473.html