杭电多校第十场 hdu6435 CSGO 二进制枚举子集

CSGO

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 459    Accepted Submission(s): 227

Problem Description

You are playing CSGO.
There are n Main Weapons and m Secondary Weapons in CSGO. You can only choose one Main Weapon and one Secondary Weapon. For each weapon, it has a composite score S.
The higher the composite score of the weapon is, the better for you.
Also each weapon has K performance evaluations x[1], x[2], …, x[K].(range, firing rate, recoil, weight…)
So you shold consider the cooperation of your weapons, you want two weapons that have big difference in each performance, for example, AWP + CZ75 is a good choose, and so do AK47 + Desert Eagle.
All in all, you will evaluate your weapons by this formula.(MW for Main Weapon and SW for Secondary Weapon)

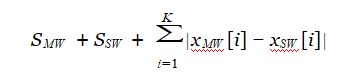
Now you have to choose your best Main Weapon & Secondary Weapon and output the maximum evaluation.

 

Input

Multiple query.
On the first line, there is a positive integer T, which describe the number of data. Next there are T groups of data.
for each group, the first line have three positive integers n, m, K.
then, the next n line will describe n Main Weapons, K+1 integers each line S, x[1], x[2], …, x[K]
then, the next m line will describe m Secondary Weapons, K+1 integers each line S, x[1], x[2], …, x[K]
There is a blank line before each groups of data.
T<=100, n<=100000, m<=100000, K<=5, 0<=S<=1e9, |x[i]|<=1e9, sum of (n+m)<=300000

 

Output

Your output should include T lines, for each line, output the maximum evaluation for the corresponding datum.

 

Sample Input

2
2 2 1
0 233
0 666
0 123
0 456
2 2 1
100 0 1000 100 1000 100
100 0

 

Sample Output

543 2000

题意：求

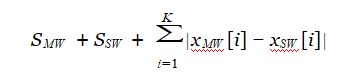
表达式的最大值

分析：

　　上面的式子如果要去最大值，肯定是Xmw[i]和Xsw[i]一个取最大值一个取最小值。

　　也就是加上最大值减去最小值

　　如何取出最大值和最小值？

　　考虑枚举上面式子的每一个Xmw[i]和Xsw[i]的状态，每个Xmw[i]和Xsw[i]都有可能被加上或者减去

　　我们可以做一次二进制枚举出每个子集，这样可以求出子集中mw和sw可能的最大值和最小值

　　而Smw和Ssw是都要加上的，所以我们将Smw和Ssw都放进mw和sw的数组但是放在不同位置

参考博客：https://blog.csdn.net/qq_40774175/article/details/81950796

AC代码：

#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <string>
#include <bitset>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#define ls (r<<1)
#define rs (r<<1|1)
#define debug(a) cout << #a << " " << a << endl
using namespace std;
typedef long long ll;
const ll maxn = 1e5+10;
const ll mod = 998244353;
const double pi = acos(-1.0);
const double eps = 1e-8;
ll a[maxn][8], b[maxn][8];
int main() {
    ios::sync_with_stdio(0);
    ll T;
    cin >> T;
    while( T -- ) {
        ll n, m, k;
        cin >> n >> m >> k;
        for( ll i = 0; i < n; i ++ ) {
            cin >> a[i][0];
            for( ll j = 0; j < k; j ++ ) {
                cin >> a[i][j+2];
            }
        }
        for( ll i = 0; i < m; i ++ ) {
            cin >> b[i][1];
            for( ll j = 0; j < k; j ++ ) {
                cin >> b[i][j+2];
            }
        }
        ll ans = -1e18;
        for( ll s = 0; s < 1<<(k+2); s ++ ) {
            ll maxa = -1e18, mina = 1e18;
            ll maxb = -1e18, minb = 1e18;
            for( ll i = 0; i < n; i ++ ) {
                ll tmp = 0;
                for( ll j = 0; j < k+2; j ++ ) {
                    if( s&(1<<j) ) {
                        tmp += a[i][j];
                    } else {
                        tmp -= a[i][j];
                    }
                }
                maxa = max(maxa,tmp);
                mina = min(mina,tmp);
            }
            for( ll i = 0; i < m; i ++ ) {
                ll tmp = 0;
                for( ll j = 0; j < k+2; j ++ ) {
                    if( s&(1<<j) ) {
                        tmp += b[i][j];
                    } else {
                        tmp -= b[i][j];
                    }
                }
                maxb = max(maxb,tmp);
                minb = min(minb,tmp);
            }
            ans = max(ans,max(maxa-minb,maxb-mina));
        }
        cout << ans << endl;
    }
    return 0;
}