[Noi2016]区间

题目描述

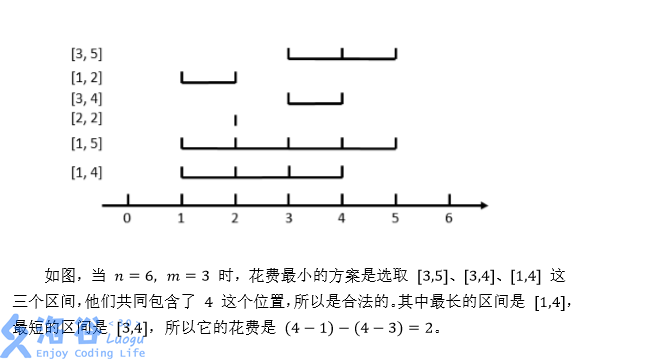
在数轴上有 n个闭区间 [l1,r1],[l2,r2],...,[ln,rn]。现在要从中选出 m 个区间，使得这 m个区间共同包含至少一个位置。换句话说，就是使得存在一个 x，使得对于每一个被选中的区间 [li,ri]，都有 li≤x≤ri。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 [li,ri] 的长度定义为 ri−li，即等于它的右端点的值减去左端点的值。

求所有合法方案中最小的花费。如果不存在合法的方案，输出 −1。

输入输出格式

输入格式：

第一行包含两个正整数 n,m用空格隔开，意义如上文所述。保证 1≤m≤n

接下来 n行，每行表示一个区间，包含用空格隔开的两个整数 li 和 ri 为该区间的左右端点。

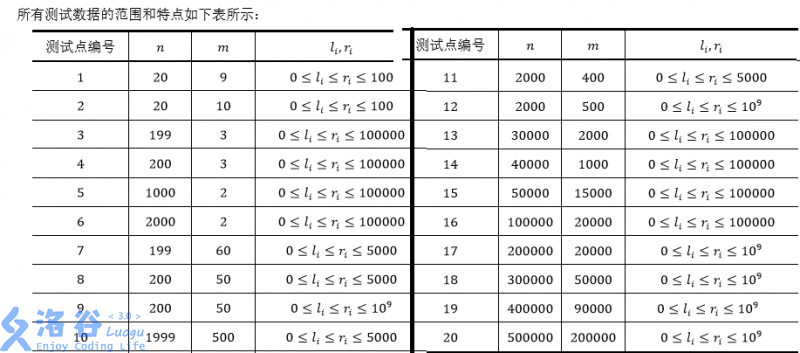
N<=500000,M<=200000,0≤li≤ri≤10^9

输出格式：

只有一行，包含一个正整数，即最小花费。

输入输出样例

输入样例#1：

6 3
3 5
1 2
3 4
2 2
1 5
1 4

输出样例#1：

2

说明

题解：

离散化+线段树维护+决策单调性

先将数据离散，但区间长不变。

按区间长从小到大排序，可知单调性：当最大值大于m时，再增加区间不会使答案减小，即当前最优解(意思是不必在往后走，而不是全局最优)。

具体实现与单调队列一样，不过区间的和用线段树维护，当小于m时入队

将当前答案与ans比较记下，队首出队，继续执行。

注意队尾要小于等于n，与ans比较时，区间和必须大于m

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 struct Messi
 {
     int x,y,l;
 }a[];
 int k,p[],lazy[],c[],n,m,ans;
 bool vis[];
 int find(int x)
 {int l,r;
     l=;r=k;
     while (l<r)
     {
         int mid=(l+r)/;
         if (p[mid]>=x) r=mid;
         else l=mid+;
     }
     return l;
 }
 bool cmp(Messi a,Messi b)
 {
     return (a.l<b.l);
 }
 void pushdown(int rt)
 {
     if (lazy[rt]!=)
     {
         lazy[rt*]+=lazy[rt];
         lazy[rt*+]+=lazy[rt];
         c[rt*]+=lazy[rt];
         c[rt*+]+=lazy[rt];
         lazy[rt]=;
     }
 }
 void update(int rt,int l,int r,int L,int R,int k)
 {
     if (l!=r) pushdown(rt);
     if (l>=L&&r<=R)
     {
         c[rt]+=k;
         lazy[rt]+=k;
         return;
     }

     int mid=(l+r)/;
      if (L<=mid) update(rt*,l,mid,L,R,k);
      if (R>mid) update(rt*+,mid+,r,L,R,k);
      c[rt]=max(c[rt*],c[rt*+]);
 }
 int main()
 {int i,j;
     cin>>n>>m;
     for (i=;i<=n;i++)
     {
         scanf("%d%d",&a[i].x,&a[i].y);
         {
             k++;
             p[k]=a[i].x;
         }
         {
             k++;
             p[k]=a[i].y;
         }
         a[i].l=a[i].y-a[i].x;
     }
      sort(p+,p+k+);
      for (i=;i<=n;i++)
      {
          a[i].x=find(a[i].x);
          a[i].y=find(a[i].y);
      }
      sort(a+,a+n+,cmp);
      j=;
      ans=2e9;
      for (i=;i<=n;i++)
      {
       if (j==n) break;
          while (c[]<m&&j<n)
          {
          j++;
              update(,,k,a[j].x,a[j].y,);
          }
          if (c[]>=m) ans=min(a[j].l-a[i].l,ans);
          update(,,k,a[i].x,a[i].y,-);
      }
      if (ans==2e9)
      cout<<-;
      else
      cout<<ans;
 }