LeetCode.62——不同路径

---

• 问题描述：

  一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

  机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

  问总共有多少条不同的路径？

  

  例如，上图是一个7 x 3 的网格。有多少可能的路径？LeetCode原题

• 问题分析：

  这是一个比较简单的动态规划问题，由于没有障碍 (不同路径2 网格中有障碍),

  由于每一步都只能向右或者向下，那很明显，可以知道第一行和第一列的每一个格子都是1：

  

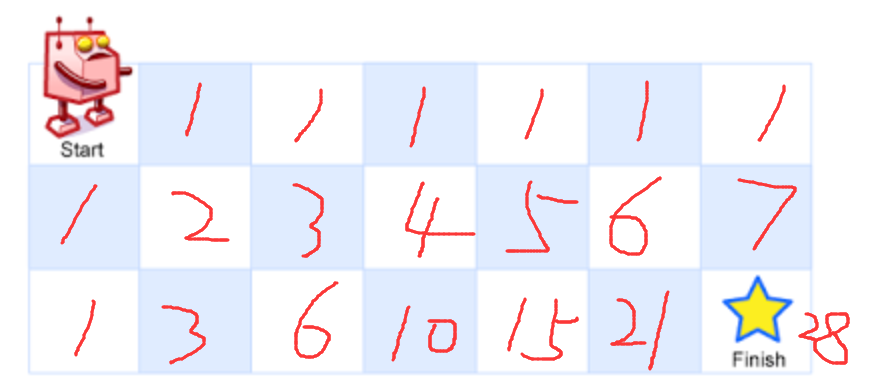
  由于只能向右和向下，能达到2号位置的路径只有两种，右→下 或者 下→右。同理，第一行第一列以外的其他任何一个位置的路径数，都等于当前位置前面和上面的路径和。这样就可以得到最终的路径：

  dp[m-1][n-1] = dp[m-1][n-2] + dp[m-2][n-1]
  

• 代码实现：

  public class UniquePaths_62{
      public static void main(String[] args) {
          Solution4 solution = new Solution4();
         int res = solution.uniquePaths(1,1);
          System.out.println(res);
      }
  
  }
  
  class Solution {
      public int uniquePaths(int m, int n) {
          //1.初始化第一行第一列
          int[][] dp = new int[m][n];
          for (int i = 0; i < dp.length; i++) {
              for (int j = 0; j < dp[0].length; j++) {
                  dp[0][j] = 1;
                  dp[i][0] = 1;
              }
          }
  
          for (int i = 1; i < dp.length; i++) {
              for (int j = 1; j < dp[0].length; j++) {
                  dp[i][j] = dp[i][j-1] + dp[i-1][j];
              }
          }
          return dp[m-1][n-1];
      }
  }
  

  性能：

  ​ （1）时间复杂度：O（m*n）

  ​ （2）空间复杂度：O（m*n）

  ---

• 最后 ：

  由于个人水平有限，博文中难免有错误或表达不准确之处，欢迎各位大佬批评指正。如有更好的方法，欢迎评论区留下你的高见，欢迎转载转发，记得注明出处。码字不易，如有帮助，欢迎打赏一杯熬夜咖啡，谢谢老板~~~