自动完成 APP【字典树（Trie树）+dfs】

自动完成 APP

传送门  来源：upc12786

题目描述

奶牛 Bessie 很喜欢用手机上网聊天，但她的蹄子太大，经常会按到好几个键造成不必要的麻烦（丢死人了，你下辈子还是不要当奶牛了）。于是 Farmer John 给她专门设计了一套「自动完成 APP」。这个 APP 能够连接到在线词典来获取词库（词库的来源是 Bessie 常用的 n 个单词），并且有着自动补全的功能。当 Bessie 想打出她的一个常用单词时，她只需输入这个单词的某个前缀，并询问词库中拥有这个前缀的字典序第 k 小的单词，APP 就会返回这是词库中的第几个单词。

Farmer John 是个大忙人，所以编写 APP 的任务自然就交给了你。

输入

第一行两个整数 n,m，表示词库的单词个数和 Bessie 的询问次数。

接下来 n 行，每行一个字符串，表示 Bessie 的常用单词，输入的第 i 个字符串在词库中编号为 i。

接下来 m 行，每行一个整数 k 和一个字符串 S，表示 Bessie 的询问，意义是询问词库中以 S 为前缀的字典序第 k 小的单词在词库中的编号。

输出

对于每次询问输出一个整数，表示以S为前缀的字典序第 k 小的单词在词库中的编号；如果不存在这样的单词，输出 −1。

样例输入

10 3
dab
ba
ab
daa
aa
aaa
aab
abc
ac
dadba
4 a
2 da
4 da

样例输出

3
1
-1

提示：

(1) 以 a 为前缀的单词有 {aa,aaa,aab,ab,abc,ac}，其中字典序第 4 小的是 ab，是词库的第 3 个单词。

(2) 以 da 为前缀的单词有 {daa,dab,dadba}，其中字典序第 2 小的是 dab，是词库的第 1 个单词；没有第 4 小的单词。

对于 20% 的数据，1≤ 词库的字母总量,询问的字母总量 ≤103。

对于 100%的数据，1≤ 词库的字母总量,询问的字母总量 ≤106，保证词库里的单词两两不同，所有字符串只包含小写字母。

思路：

如果对字典树有了解，开始能感觉到是个字典树的板子题加上dfs能解决，但TLE。

看了题解，先用字典树把所有单词存起来，再跑一次dfs给每个单词的结尾附上id（连续的），就可以直接求了，具体看解析。

思路解析：（输入单词：dab ba ab daa aa aaa）

1、建立字典树（具体怎么建字典树：浅谈Trie树（字典树）写的很好）

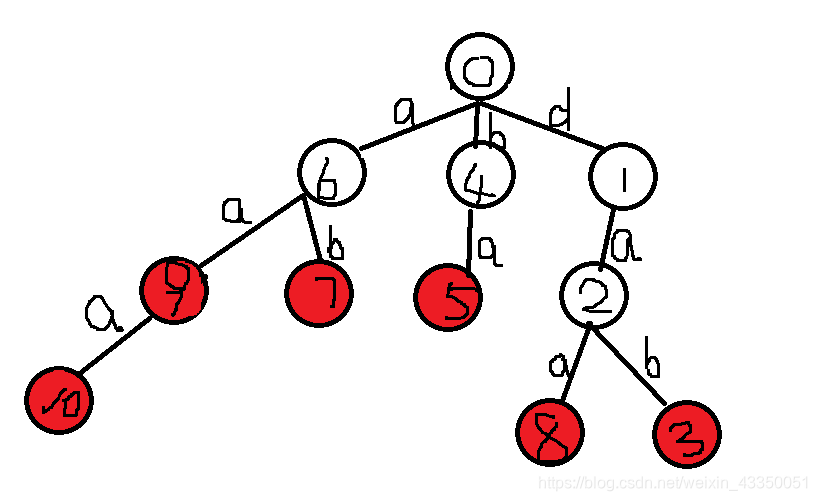
用sum数组记录每个点是几个单词的前缀，例如sum[4]=1。

如果单词结束还要用flag1数组表示他是第几个单词，便于最后输出，例如flag1[10]=6（因为他是第六个单词嘛）。

这两点在建字典树的时候经常用到，不难理解。

上图中红色点表示其上面字符串构成了一个单词。

2、dfs给红色点赋id（蓝色数字为赋给的id，有规律便于结题）

蓝色的数字表示赋给的id，存入数组num中，如果是红点的话还要用数组dir存入其root值（root值就是圈中心的数字）。

例如 root=3时 id=6  则：

num[3]=6   dir[6]=3;

root=1 时 id=5

只需要num[1]=5而不需要存入dir数组中，因为root不是红点。

3.1、根据输入的字符串判断是否有存在单词满足该前缀的可能性

例如输入：1 fffffff (这不是乔碧萝殿下的坦克！！)

从图中可以看出不可能构成单词，可以直接输出-1。

3.2、如果满足条件，返回root的值

例如输入：3 b

返回root的值： 4 判断sun[4]和k的大小关系，如果不满足输出-1。

4、如果上面条件不能输出-1，那就意味着肯定能找到第k小的单词。

直接输出flag1[ dir[ num[ root ] + k - 1 ] ]就是结果。我当时就看到就很懵逼，但分析完这个公式你会感觉整个解题思路超级紧密。

分析公式：flag1[ dir[ num[ root ] + k - 1 ] ]

1、num[ root ] + k - 1 表示的是一个数的 id

2、把id放进num[ ]中即 num[id]是不是就表示这个数的root值

3、再把root放进flag1[]中即flag1[root]是不是表示第几个输入的单词

类似链式前向星的head数组和edge数组的关系，就是很巧妙。

分析完公式，超级佩服这个思路，感谢：溺生。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int MAX=1e6;
int trie[MAX+5][35];
char a[MAX+5];
int n,m,k;
int top;
int flag[MAX+5],flag1[MAX+5],num[MAX+5],dir[MAX+5];
int sum[MAX+5];
void Insert(char a[],int k1) ///建字典树
{
    int la=strlen(a);
    int root=0;
    for(int i=0;i<la;i++){
        int id=a[i]-'a';
        if(!trie[root][id]) trie[root][id]=++top;
        sum[trie[root][id]]++;
        root=trie[root][id];
    }
    flag[root]=1; ///标记该root点有单词结束
    flag1[root]=k1; ///给root点赋输入的顺序，便于输出
}
int cnt;
void dfs(int res) ///dfs给所有的root点赋上图id值
{
    if(flag[res]){
        dir[++cnt]=res;
        num[res]=cnt;
    }else{
        num[res]=cnt+1;
    }
    for(int i=0;i<26;i++){
        if(trie[res][i]){
            dfs(trie[res][i]);
        }
    }
}
int Find(char a[])///判断输入的前缀是不是有构成单词的可能性，如果有返回最后的root值，没有返回-1
{
    int la=strlen(a);
    int root=0;
    for(int i=0;i<la;i++){
        int id=a[i]-'a';
        if(!trie[root][id]){
            return -1;
        }
        root=trie[root][id];
    }
    return root;
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=0;i<n;i++){
        scanf("%s",a);
        Insert(a,i+1);
    }
    dfs(0);
    for(int i=0;i<m;i++){
        scanf("%d%s",&k,a);
        int res=Find(a);
        if(res==-1){
            printf("-1\n");
        }else{
            if(sum[res]<k){
                printf("-1\n");
            }else{
                printf("%d\n",flag1[dir[num[res]+k-1]]);///输出结果
            }
        }
    }
    return 0;
}