二次代价函数、交叉熵(cross-entropy)、对数似然代价函数（log-likelihood cost）(04-1)

二次代价函数

$C = \frac{1} {2n} \sum_{x_1,...x_n} \|y(x)-a^L(x) \|^2$

其中，C表示代价函数，x表示样本，y表示实际值，a表示输出值，n表示样本的总数；整个的意思就是把n个y-a的平方累加起来，再除以2求一下均值。

为简单起见，先看下 一个样本 的情况，此时二次代价函数为：$C = \frac{(y-a)^2} {2}$

$a=\sigma(z), z=\sum w_j*x_j +b$  ，其中a就代表激活函数的输出值，这个符号$\sigma$代表sigmoid函数将变量映射到0-1的$S$型光滑的曲线，z是上一层神经元信号的总和

假如我们使用梯度下降发(Gradient descent)来调整权值参数的大小，权值w和权值b的梯度推到如下(求导数)：

$\frac {\partial C} {\partial w} = (a-y)\sigma' (z)x$    $\frac {\partial C} {\partial b} = (a-y)\sigma' (z)$

其中，z表示神经元的输入，$\sigma$表示激活函数sigmoid。可以看出，w和b的梯度跟激活函数的梯度成正比，激活函数的梯度越大，w和b的大小调整越快，训练收敛的就越快。

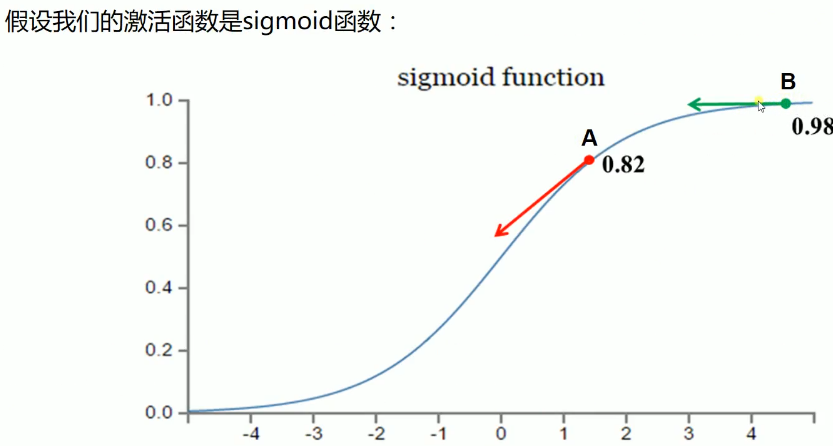
假设我们激活函数输出的值目标是收敛到1，A点离目标较远，梯度较大，权值调整比较大。B点为0.98离目标比较近，梯度比较小，权值调整比较小，调整方案合理。

假设我们激活函数输出的值目标是收敛到0，A点离目标较远，梯度较大，权值调整比较大。B点为0.98离目标比较远，梯度比较小，权值调整比较小，调整方案不合理，B点要经过非常长的时间才会收敛到0，而且B点很可能成为不收敛的点。

交叉墒代价函数(cross-entropy)

由于上边的问题，我们换一种思路，我们不改变激活函数，而是改变代价函数，改用交叉墒代价函数：

$C = -\frac{1}{n} \sum_{x_1,,,x_n}, [y\ln a + (1-y) \ln(1-a)]$

其中，C表示代价函数，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。

$a=\sigma(z), z=\sum w_j*x_j +b $ $ \sigma'(z) = \sigma(z)(1-\sigma (x))$ sigmod函数的导数比较好求，这也是为什么大家用sigmoid做激活函数的原因，接下来我们看一下求导的过程

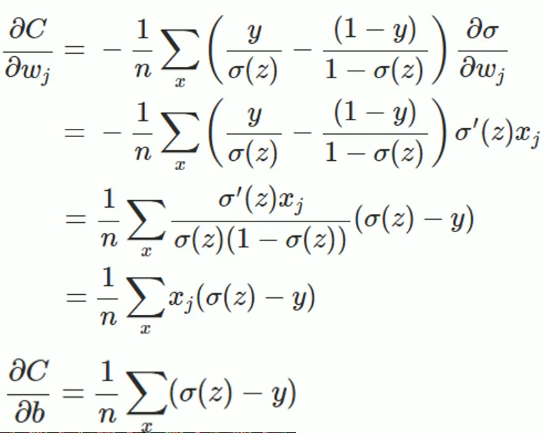
懒得敲了，直接贴个图过来，之后闲了在敲一遍，上边就是求导的推导过程，从最后的式子可以看出：权值w和偏执值b的调整与$\sigma '(z)$无关，另外，梯度公式中的$\sigma (z)-y$表示输出值与实际值放入误差。所以当误差越大时，梯度就越大，参数w和b的调整就越快，训练的速度也就越快。

总结：当输出神经元是线性的，那么二次代价函数就是一种合适的选择。如果输出神经元是S型函数，那么比较适合交叉墒代价函数。

对数似然代价函数（log-likelihood cost）

对数似然函数常用来作为softmax回归的代价函数，如果输出层神经元是sigmoid函数，可以使用交叉墒代价函数。而深度学习中更普遍的做法是将softmax作为最后一层，此时常用的代价函数是对数似然代价函数。

对数似然代价函数与softmax的组合和交叉墒与sigmoid函数的组合非常相似。对数似然代价函数在二分类时可以化简为交叉墒代价函数的形式。

在TensorFlow中用：

tf.nn.sigmoid_cross_entropy_with_logits()来表示跟sigmoid搭配使用的交叉墒。

tf.nn.softmax_cross_entropy_with_logits()来表示跟softmax搭配使用的交叉墒。