【面试QA-基本模型】LSTM

目录

• 为什么传统 CNN 适用于 CV 任务，RNN 适用于 NLP 任务
• RNN 原理
• LSTM 原理
• GRU 原理
• RNN BPTT
• LSTM 如何解决 RNN 的梯度消失问题
• 怎样增加 LSTM 的长距离特征提取能力

为什么传统 CNN 适用于 CV 任务，RNN 适用于 NLP 任务

从模型特点上来说：

• 对于 CNN 每一个卷积核都可以看作是一个滤波器，卷积运算的本质是互相关运算，每个卷积核仅对于具有特定特征具有较大的激活值，而且 CNN 有参数共享和局部连接的特点，能够提取图像上不同位置的同一个特征，即 CNN 具有平移不变性

• RNN 的特点在于其是一个时序模型，在对每个神经元不仅可以接收当前时刻的输入信息，还将接收上一个时刻的该神经元的输出信息，具有短期记忆能力。这在用于 NLP 任务时相当于隐含着建立了一个语言模型，这对词序具有很强的区分能力。而 CNN 和 DNN 均类似词袋模型，丢失的词序特征。

从数据特征上来说

• 图像矩阵中的每个元素为图像中的像素值，每个像素与其周围元素都是高度相关的
• 文本矩阵中的数据为词的 embedding 向量，每个元素在词向量内与词向量间的相邻元素的关联性是不同的，因此 CNN 用于 NLP 任务常使用的是一维卷积

RNN 原理

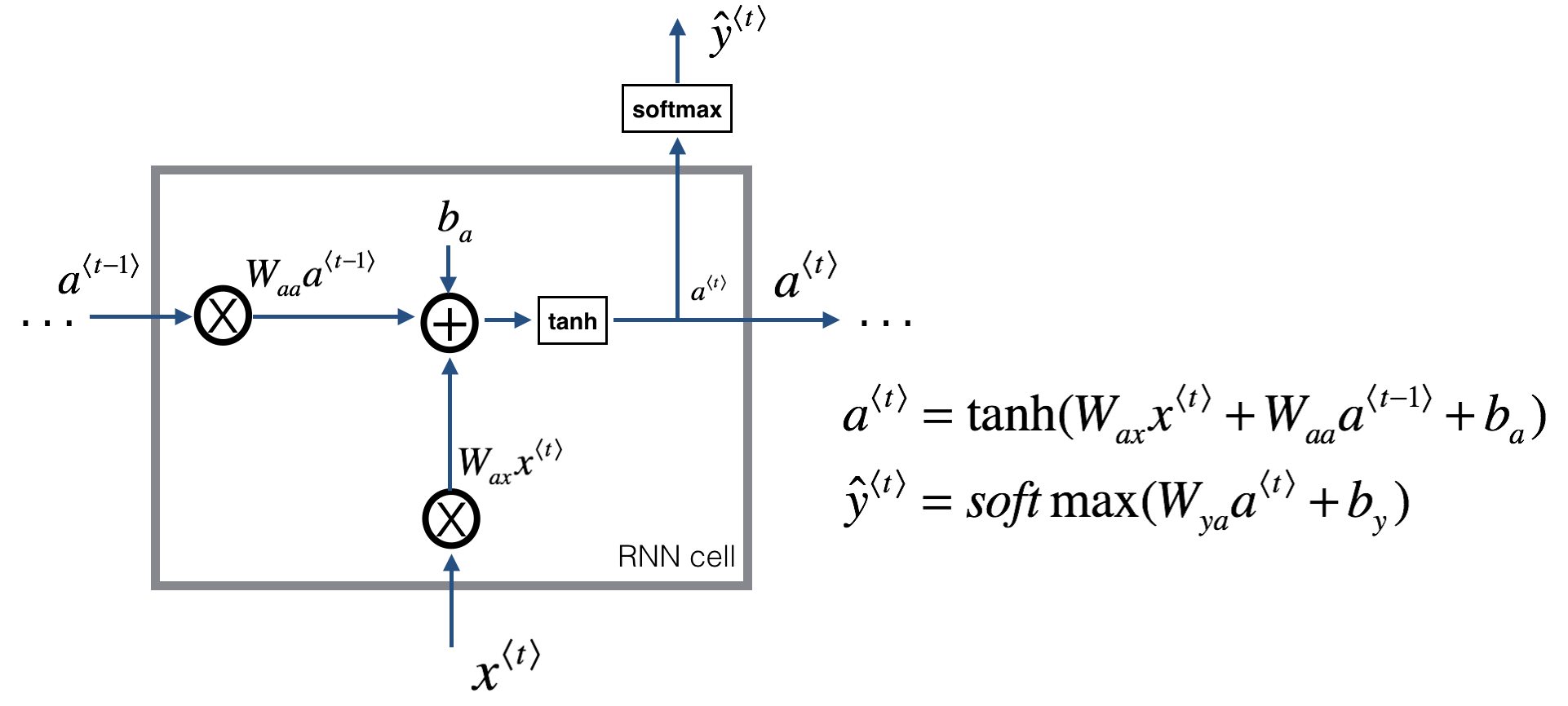
\(\hat y\) 部分的激活函数可以根据下游任务设置

LSTM 原理

• 三个门：[output_dim + input_dim, 1]
• 更新门位置的全连接层：[output_dim + input_dim, output_dim]
  
  

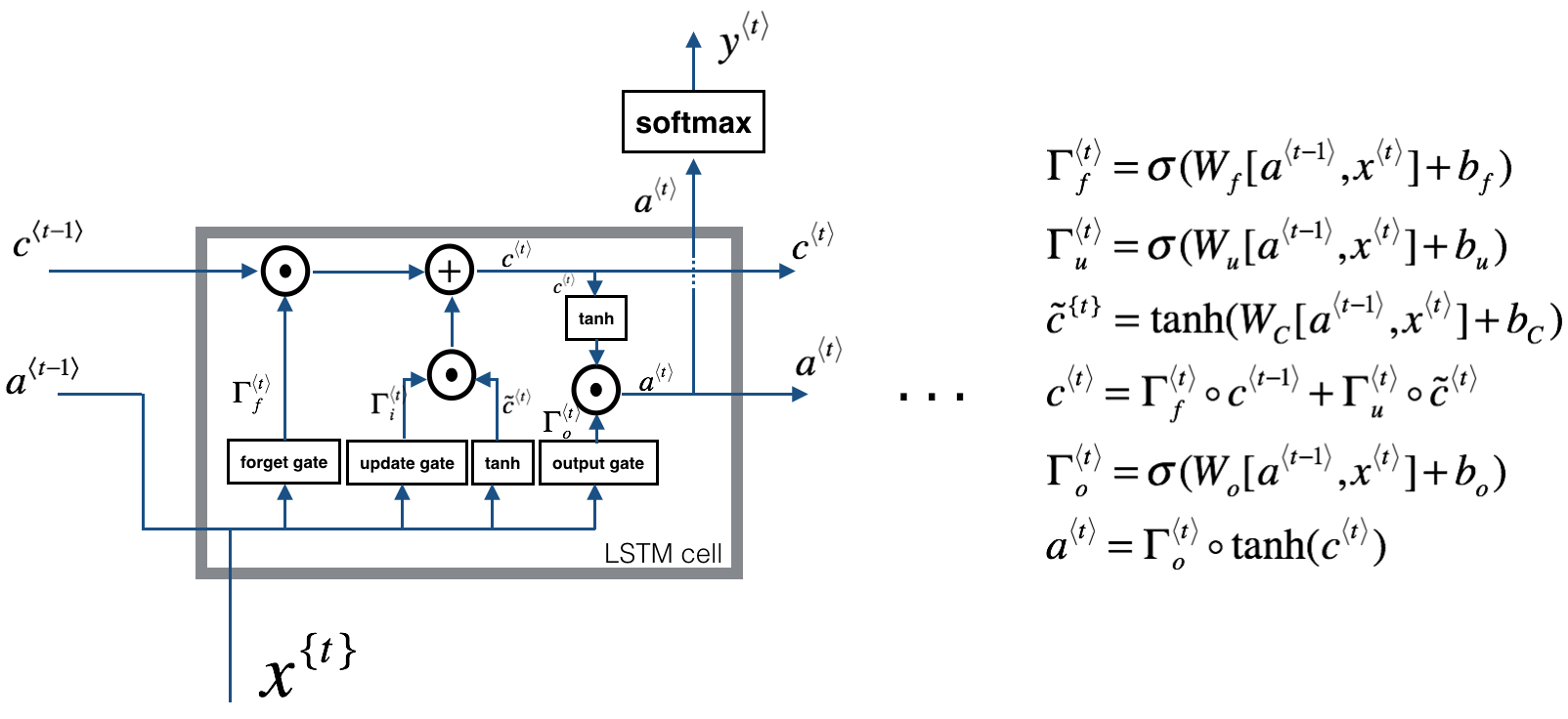
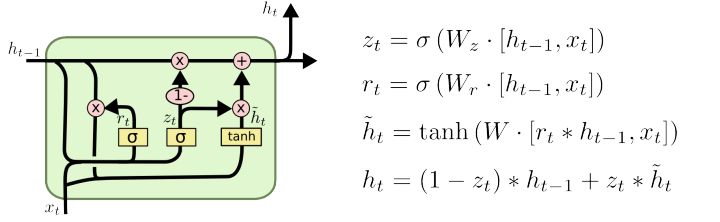
GRU 原理

• 两个门：[output_dim + input_dim, 1]
• 全连接层：[output_dim + input_dim, output_dim]
  
  

RNN BPTT

- 假设$t$时刻的损失函数为$L_t$，以 $W_{aa}$，$W_{ax}$，$W_{ya}$ 为例
$$ \begin{aligned}
&\frac{\delta L_t}{\delta W_{ya}} = \frac{\delta L_3}{\delta \hat{y}_t}\frac{\delta \hat{y}_t}{\delta W_{ya}} \\
&\frac{\delta L_t}{\delta W_{aa}} = \frac{\delta L_t}{\delta \hat{y}_t}\frac{\delta \hat{y}_t}{\delta a_{t}}(\frac{\delta a_{t}}{\delta W_{aa}} + \frac{\delta a_{t}}{\delta a_{t-1}}\frac{\delta a_{t-1}}{\delta W_{aa}} + ...)\\
&\frac{\delta L_t}{\delta W_{ax}} = \frac{\delta L_3}{\delta \hat{y}_t}\frac{\delta \hat{y}_t}{\delta a_{t}}(\frac{\delta a_{t}}{\delta W_{ax}} + \frac{\delta a_{t}}{\delta a_{t-1}}\frac{\delta a_{t-1}}{\delta W_{ax}} + ...)
\end{aligned}$$

• 对于任意时刻t对 \(W_x\)，\(W_s\) 求偏导的公式为：

\[\begin{aligned}
&\frac{\delta L_t}{\delta W_{aa}} = \sum_{k=0}^{t}\frac{\delta L_t}{\delta y_t}\frac{\delta y_t}{\delta a_t}( \prod_{j=k+1}^t\frac{\delta a_j}{\delta a_{j-1}} ) \frac{\delta a_k}{\delta W_{aa}}\\
&\frac{\delta L_t}{\delta W_{aa}} = \sum_{k=0}^{t}\frac{\delta L_t}{\delta y_t}\frac{\delta y_t}{\delta a_t}( \prod_{j=k+1}^t\frac{\delta a_j}{\delta a_{j-1}} ) \frac{\delta a_k}{\delta W_{aa}}
\end{aligned}\]

• 其中\(\frac{\delta a_j}{\delta a_{j-1}}\)和\(\frac{\delta a_k}{\delta W_{aa}}\)还存在\(tanh'\)的导数项，而\(tanh'\)的值域为\((0, 1)\)。随着时间步的增长，累乘项会趋于 0，出现梯度消失的问题

LSTM 如何解决 RNN 的梯度消失问题

• RNN 的激活函数为 \(tanh\)，而 \(tanh\) 的导数取值范围为 \([0, 1]\)，在时间上的反向传播会存在时间上的梯度累乘项，时间步长了会导致梯度累乘而消失
• LSTM 通过引入全局信息流，在时间维度上引入残差结构，残差结构的引入就使得链式求导过程中引入了一个求和项，从反向传播的求导来看，最多只有两个激活函数的导数累乘，因此远距离的梯度通常都可以正常传播，减弱了梯度消失问题

怎样增加 LSTM 的长距离特征提取能力

• Dilated RNN：Dilated CNN 为空洞卷积，Dilated RNN 则是在时间维度上空洞，浅层部分的为传统 RNN，每个时间步都循环，深层的循环周期更长，增大时间维度上的“感受野”