关于PCA的几何表示——MATLAB实现

　　关于PCA的一道练习题。这个折腾了好久。。。终于做出来像样的图，开始的时候忘记对原始数据标准化，怎么也不对。经过标准化之后，做的图看着还可以，有错误请指出！

　　MATLAB代码PCA.m：

clear
clc
% 生成training sample
MU1 = [6 10]';
MU2 = [6 20]';
SIGMA1 = [2 4; 4 9];
SIGMA2 = [2 4; 4 9];

M1 = mvnrnd(MU1,SIGMA1,1000);
M2 = mvnrnd(MU2,SIGMA2,1000);
M = [M1;M2];
MEAN = mean(M);
% 标准化
std_M(:,1) = (M(:,1)-MEAN(1))/std(M(:,1));
std_M(:,2) = (M(:,2)-MEAN(2))/std(M(:,2));

%计算相关系数矩阵
C = (std_M'*std_M)/2000;
%计算特征值和特征向量
[V, D] = eig(C);
%v为最大特征值对应的特征向量
v = V(:,2);
%求原数据点在特征向量轴映射后的坐标
for (i=1:2000)
    VD(i,:) = dot(v,M(i,:))*v';
end
%画在同一坐标系下
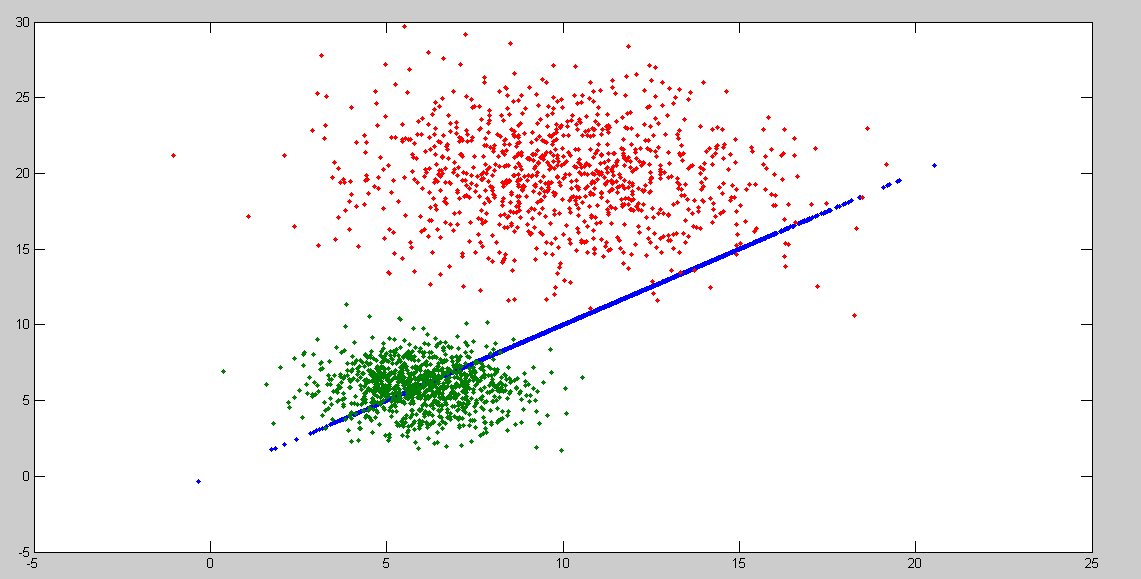
plot(VD(:,1),VD(:,2),'.',M1,M2,'.')

　　输出：