HDU 5015 233 Matrix --矩阵快速幂

题意：给出矩阵的第0行（233,2333,23333,...）和第0列a1,a2,...an（n<=10，m<=10^9），给出式子： A[i][j] = A[i-1][j] + A[i][j-1]，要求A[n][m]。

解法：看到n<=10和m<=10^9 应该对矩阵有些想法，现在我们假设要求A[a][b],则A[a][b] = A[a][b-1] + A[a-1][b] = A[a][b-1] + A[a-1][b-1] + A[a-2][b] = ...

这样相当于右图：，红色部分为绿色部分之和，而顶上的绿色部分很好求，左边的绿色部分(最多10个)其实就是：A[1][m-1],A[2][m-1]..A[n][m-1],即对每个1<=i<=n, A[i][m]都可由A[1][m-1],A[2][m-1]..A[n][m-1]，于是建立12*12的矩阵：

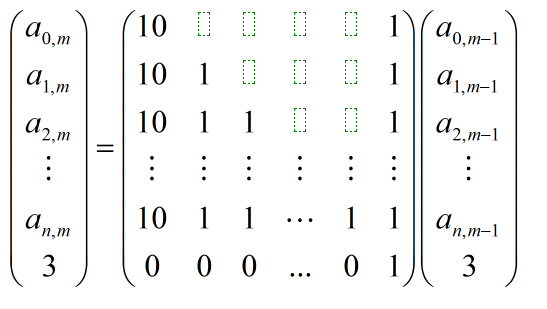，将中间矩阵求m-1次幂，与右边[A[0][1],A[1][1]..A[n][1],3]^T相乘，结果就可以得出了。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#define Mod 10000007
#define SMod Mod
#define lll __int64
using namespace std;

int n,m;
lll a[],sum[];

struct Matrix
{
    lll m[][];
    Matrix()
    {
        memset(m,,sizeof(m));
        for(int i=;i<=n+;i++)
            m[i][i] = 1LL;
    }
};

Matrix Mul(Matrix a,Matrix b)
{
    Matrix res;
    int i,j,k;
    for(i=;i<=n+;i++)
    {
        for(j=;j<=n+;j++)
        {
            res.m[i][j] = ;
            for(k=;k<=n+;k++)
                res.m[i][j] = (res.m[i][j]+(a.m[i][k]*b.m[k][j])%SMod + SMod)%SMod;
        }
    }
    return res;
}

Matrix fastm(Matrix a,int b)
{
    Matrix res;
    while(b)
    {
        if(b&)
            res = Mul(res,a);
        a = Mul(a,a);
        b >>= ;
    }
    return res;
}

int main()
{
    int i,j;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        sum[] = ;
        for(i=;i<=n;i++)
        {
            scanf("%I64d",&a[i]);
            sum[i] = (sum[i-] + a[i]);
        }
        lll suma = sum[n];
        if(m == )
        {
            printf("%I64d\n",(233LL+suma)%Mod);
            continue;
        }
        Matrix base;
        memset(base.m,,sizeof(base.m));
        for(i=;i<=n+;i++)
            base.m[i][] = 10LL;
        for(i=;i<=n+;i++)
        {
            for(j=;j<=n+;j++)
            {
                if(i >= j)
                    base.m[i][j] = 1LL;
            }
        }
        for(i=;i<=n+;i++)
            base.m[i][n+] = 1LL;
        Matrix Right;
        memset(Right.m,,sizeof(Right.m));
        Right.m[][] = 233LL;
        for(i=;i<=n+;i++)
            Right.m[i][] = (233LL+sum[i-])%Mod;
        Right.m[n+][] = 3LL;
        Matrix ans = fastm(base,m-);
        ans = Mul(ans,Right);
        printf("%I64d\n",ans.m[n+][]%Mod);
    }
    return ;
}