[LOJ#2732] 「JOISC 2016 Day 2」雇佣计划

参考博文

（不过个人感觉我讲的稍微更清楚一点）

---

题目就是让我们求图中满足数值大于等于B的连通块数量

然后我们可以尝试转换为求连通块两端所产生的“谷”的数量，显然一个连通块对谷可以贡献2的答案，最终答案就是谷的数量除以2

（下图为查询$B_i$大小为4时的情况，每一个箭头代表一个谷）

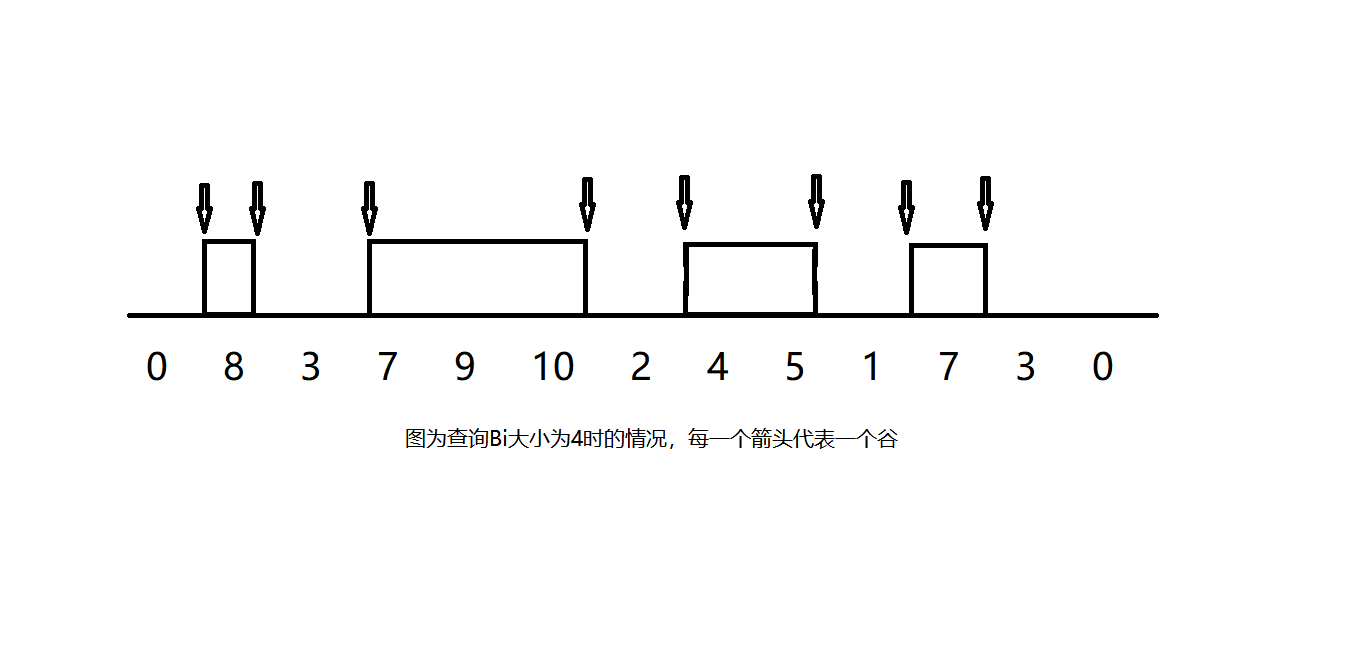
发现每两个数中间的空格都是有可能产生谷的，所以我们只需要维护有多少个空格满足产生谷的条件即可

记一个空格左边的数字为X，右边的数字为Y，当前询问为B，观察发现，当且仅当满足下列条件时，这个空格可以成为谷

$$min(X,Y)+1 \leq B \leq max(X,Y)$$

我们需要一种可以在$logn$的复杂度内维护满足上述条件点的数量，支持单点修改区间查询的数据结构，发现树状数组可以很好的满足这个要求、

我们把这个询问条件差分一下扔到树状数组里维护即可

一些注意点：

　　开始更新的时候要把0和n+1这两个节点也算进去，以免漏记录两端的“谷”

　　观察到$a_i$,$b_i$很大，我们需要进行必要的离散化

代码：

 //hgs AK IOI,IMO,ICHO,IPHO
 #include<bits/stdc++.h>
 #define writeln(x)  write(x),puts("")
 #define writep(x)   write(x),putchar(' ')
 using namespace std;
 inline int read(){
     int ans=,f=;char chr=getchar();
     while(!isdigit(chr)){if(chr=='-') f=-;chr=getchar();}
     while(isdigit(chr)){ans=(ans<<)+(ans<<)+chr-;chr=getchar();}
     return ans*f;
 }void write(int x){
     if(x<) putchar('-'),x=-x;
     if(x>) write(x/);
     putchar(x%+'');
 }const int M= 6e5+;
 int s[M],n,m,x,y,z,b[M],len,v[M];
 struct P{int opt,x,y;}q[M];
 #define low(x) (x&-x)
 inline int  GetNum(int x){return lower_bound(b+,b+len+,x)-b;}
 inline void Update(int x,int y){for(++x;x<=n*;x+=low(x))s[x]+=y;}
 inline int  Query(int x){int ans=;for(++x;x;x-=low(x))ans+=s[x];return ans;}
 inline void Init(){int tot=;//离散化 + 树状数组初始化
     for(int i=;i<=n;i++)b[++tot]=v[i];
     for(int i=;i<=m;i++)if(q[i].opt==)b[++tot]=q[i].x;else b[++tot]=q[i].y;
     sort(b+,b+tot+),len=unique(b+,b+tot+)-b-;
     for(int i=;i<=n;i++)v[i]=GetNum(v[i]);
     for(int i=;i<=m;i++)if(q[i].opt==)q[i].x=GetNum(q[i].x);else q[i].y=GetNum(q[i].y);
     for(int i=;i<=n+;i++){
         int l=v[i-],r=v[i];
         if(l>r)swap(l,r);
         Update(++l,),Update(++r,-);
     }
 }
 inline void Add(int x,int y){
     int l=v[x-],r=v[x];
     if(l>r)swap(l,r);
     Update(++l,y),Update(r+,-y);
     l=v[x],r=v[x+];
     if(l>r)swap(l,r);
     Update(++l,y),Update(r+,-y);
 }
 inline void Solve(){
     for(int i=;i<=m;i++)
         if(q[i].opt==)printf("%d\n",Query(q[i].x)/);
         else Add(q[i].x,-),v[q[i].x]=q[i].y,Add(q[i].x,);
 }
 int main(){
     n=read(),m=read();
     for(int i=;i<=n;i++)v[i]=read();
     for(int x,y,z,i=;i<=m;i++){
         if((x=read())==)q[i].opt=,q[i].x=read();
         else q[i].opt=,q[i].x=read(),q[i].y=read();
     }Init();Solve();
     return ;
 }