Codeforces 924 A Tritonic Iridescence（暴力集合交集、相等）

题目链接：点击打开链接

There is a rectangular grid of n rows of m initially-white cells each.

Arkady performed a certain number (possibly zero) of operations on it. In the i-th operation, a non-empty subset of rows Ri and a non-empty subset of columns Ci are chosen. For each row r in Ri and each column c in Ci, the intersection of row r and column c is coloured black.

There's another constraint: a row or a column can only be chosen at most once among all operations. In other words, it means that no pair of (i, j) (i < j) exists such that  or , where  denotes intersection of sets, and  denotes the empty set.

You are to determine whether a valid sequence of operations exists that produces a given final grid.

Input

The first line contains two space-separated integers n and m (1 ≤ n, m ≤ 50) — the number of rows and columns of the grid, respectively.

Each of the following n lines contains a string of m characters, each being either '.' (denoting a white cell) or '#' (denoting a black cell), representing the desired setup.

Output

If the given grid can be achieved by any valid sequence of operations, output "Yes"; otherwise output "No" (both without quotes).

You can print each character in any case (upper or lower).

Examples

input

Copy

5 8
.#.#..#.
.....#..
.#.#..#.
#.#....#
.....#..

output

Yes

input

Copy

5 5
..#..
..#..
#####
..#..
..#..

output

No

input

Copy

5 9
........#
#........
..##.#...
.......#.
....#.#.#

output

No

Note

For the first example, the desired setup can be produced by 3 operations, as is shown below.

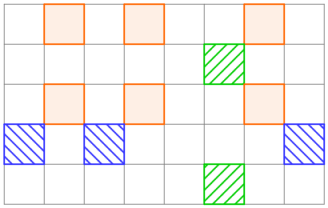
For the second example, the desired setup cannot be produced, since in order to colour the center row, the third row and all columns must be selected in one operation, but after that no column can be selected again, hence it won't be possible to colour the other cells in the center column.

官方题解：

No row or column can be selected more than once, hence whenever a row r is selected in an operation, all cells in it uniquely determine the set of columns that need to be selected — let's call it Sr.

Let's assume a valid set of operations exists. Take out any two rows, i and j. If rows i and j are selected in the same operation, we can deduce that Si = Sj; if they're in different operations, we get . Therefore, if Si ≠ Sj and  hold for any pair of rows (i, j), no valid operation sequence can be found.

Otherwise (no pair violates the condition above), a valid sequence of operations can be constructed: group all rows with the same S's and carry out an operation with each group.

Thus, it's a necessary and sufficient condition for the answer to be "Yes", that for each pair of rows (i, j), either Si = Sj or holds.

The overall complexity is O(n2m). It can be divided by the system's word size if you're a bitset enthusiast, and a lot more if hashes and hash tables release their full power.

感想：我为啥不敢写暴力呢，

代码：吸一下getchar()和bool类型的二维数组

#include <cstdio>

typedef long long int64;
static const int MAXN = 53;

static int n, m;
static bool a[MAXN][MAXN];
static int64 b[MAXN];

int main()
{
    scanf("%d%d", &n, &m); getchar();
    for (int i = 0; i < n; ++i)
        for (int j = 0; j <= m; ++j) a[i][j] = (getchar() == '#');

    for (int i = 0; i < n - 1; ++i)
        for (int j = i + 1; j < n; ++j) {
            bool all_same = true, no_intersect = true;
            for (int k = 0; k < m; ++k) {
                if (a[i][k] != a[j][k]) all_same = false;
                if (a[i][k] && a[j][k]) no_intersect = false;
            }
            if (!all_same && !no_intersect) {
                puts("No"); return 0;
            }
        }

    puts("Yes"); return 0;
}