Pyinstaller打包Web项目

最近需要用python打包一个单页面网页demo，于是准备用python包pyinstaller来打包程序。网上搜索了一下，大部分教程都是打包非web项目，这里分享一下打包简单网页demo的过程。

系统环境：win10+python3.6

一、安装pyinstaller

pip install pyinstaller

二、打包项目

1.如果是单文件项目，pyinstaller可以通过简单的命令进行python代码的打包工作，其命令为：

pyinstaller -option ***.py

　　1.1参数option可以有多个值：

　　　　-F ： 指定打包后只生成一个exe格式的文件
　　　　-D ： 生成一个文件目录包含可执行文件和相关动态链接库和资源文件等（默认选项）
　　　　-c ： –console， –nowindowed 使用控制台，无界面(默认选项)
　　　　-w ： –windowed， –noconsole 使用窗口，无控制台

　　1.2注意

　　　　①再增加一个命令参数 -w 可以保证点击生成的exe文件不会弹出黑色控制台窗口

　　　②不加 -F 参数会生成一堆文件，但是运行速度快； 加-F参数生成一个exe文件，运行起来慢

2.如果不是单文件项目，而是有多级目录（包含一些依赖的静态资源），需要自定义打包

本文以打包自己的单页面网页demo为例，各级目录结构如下：

2.1为了进行自定义配置打包，需要先输出配置文件.spec文件，执行命令：

pyi-makespec -D -w main.py

注：

-w 参数是为了保证不会产生黑色控制台窗口

-D 参数生成一个文件目录包含可执行文件和相关动态链接库和资源文件等（默认选项，也可以不加）

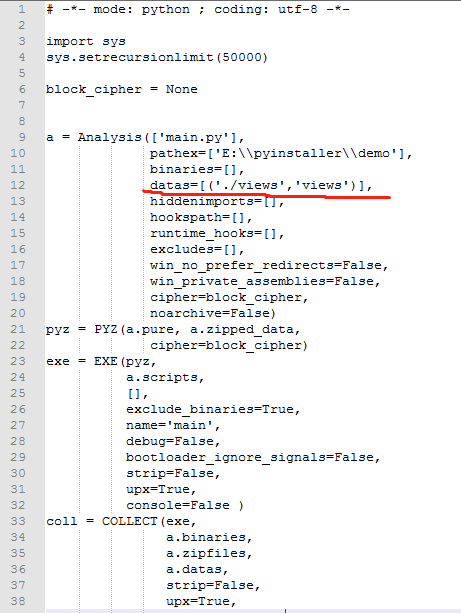
生成的 main.spec 文件如下：

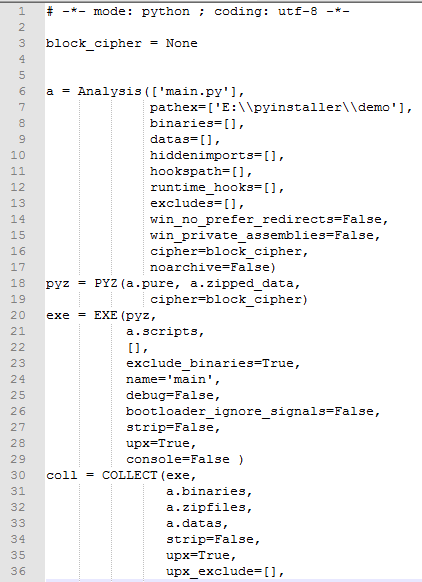
2.2为了是使打包生成后的exe文件可以加载css、js、图片等静态资源，这里需要添加依赖路径（注意：要保证自己 html 里面加载静态资源的路径是相对路径才行）。具体来说，此类资源文件的打包需要设置Analysis的datas，如下：

2.3执行打包命令：

pyinstaller main.spec

成功！

最终结果：

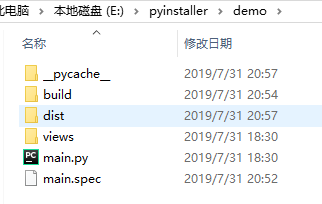
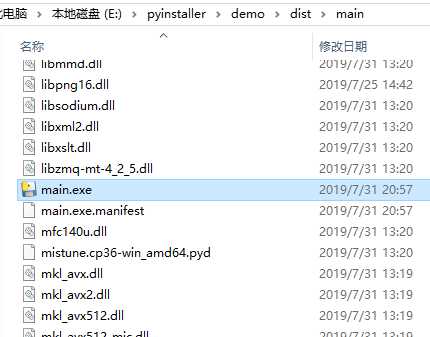
3.一些报错

①执行打包命令时，报错：RecursionError: maximum recursion depth exceeded

原因：应该是python库递归遍历太深，超过了python预设的递归深度，导致出现 “RecursionError: maximum recursion depth exceeded" 的错误

解决办法：在spec文件里设置一个大点的递归深度，在该文件第二行，添加代码如下：

import sys
sys.setrecursionlimit(50000)

②python打包pywebview时，可能会报错：WebBrowserInterop.x64.dll not found

原因：这是由于系统没有找到WebBrowserInterop.x64.dll

解决办法：将WebBrowserInterop.x64.dll文件的所在路径添加到系统环境变量里即可！

WebBrowserInterop.x64.dll文件的所在路径：

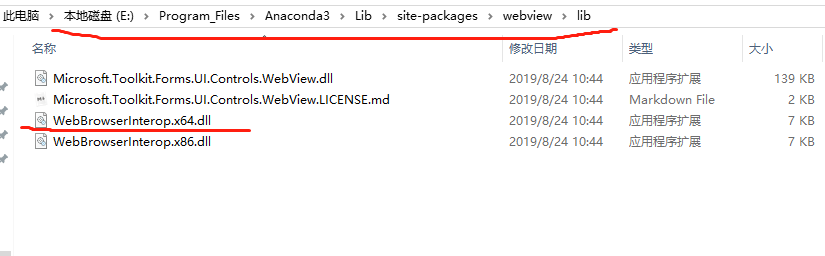
添加到系统环境变量：

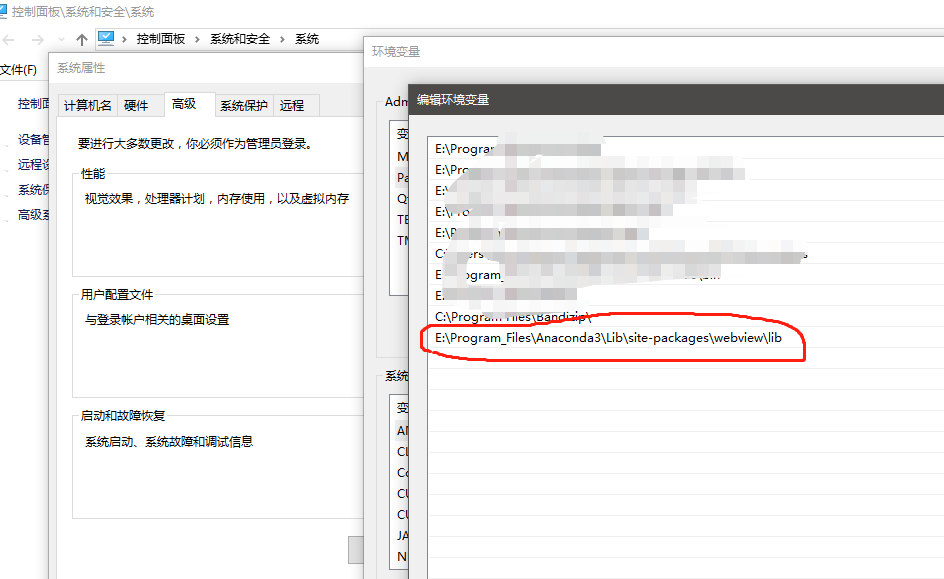
4.注意事项

①如果生成的exe文件双击无法正常运行，也没有报错提示，此时，如果想看具体报错信息，就不要直接双击执行，而是在控制台下执行