题解 SP19148【INS14G - Kill them All】

SP19148【INS14G - Kill them All】

前置知识：组合数乘法逆元

感觉其他博客讲的不是很清楚，也没有说组合数公式是怎么来的，我这样数论极菜的萌新看了好久才想明白qwq。。

还是先给出本题组合数公式C(n-1,n/2)

分析一

转化成坐标系上的移动方案问题

把第一个人杀的怪物看成横坐标，第二个人的看成纵坐标,怪物由第一个人杀向右走，反之向上走。

可知第一步一定向右，枚举终点的纵坐标m（即向上的步数），题目就变成从点(1,0)开始走到（n-m,m）不越过y=x的方案数。枚举向上步数m，总方案数为C(n-1,m)（n-1步中选m步），现在我们要减去非法方案数。

从(1,0)走到(n-m,m)的不合法方案按y=x翻转后与从(0,1)走到(n-m,m)的方案相对应

注意这里的翻转，终点是不翻转的，只翻转起点。

不合法方案为$C_{n-1}^{m-1}$（n-1步中向上走了m-1步），由此可知答案为$C_{n-1}^m-C_{n-1}^{m-1}$

公式（用i枚举终点纵坐标，0步没有不合法方案特判，0≤m（第二个人杀的次数）≤n/2）：

$C_{n-1}^0+\sum\limits_{i=1}^{\left\lfloor\frac{n}{2}\right\rfloor}(C_{n-1}^{i}-C_{n-1}^{i-1})=\sum\limits_{i=1}^{\left\lfloor\frac{n}{2}\right\rfloor}C_{n-1}^i-\sum\limits_{i=1}^{\left\lfloor\frac{n}{2}\right\rfloor-1}C_{n-1}^{i}=C_{n-1}^{\left\lfloor\frac{n}{2}\right\rfloor}$（公式来自@Alpha）

得组合数公式C(n-1,n/2)

（感谢@Alpha提供的图例与分析！）

分析二

建议可以先看看关于卡特兰数的博客中对卡特兰数的应用，和这题很像，便于理解

把题目放到笛卡尔坐标系（平面直角坐标系）中考虑（如图1），x轴表示每个怪兽，从原点出发向右上方走表示由D杀了，向右下方走表示由S杀了。相当于我从原点出发，我的轨迹不能在过程中碰到x轴。

图1

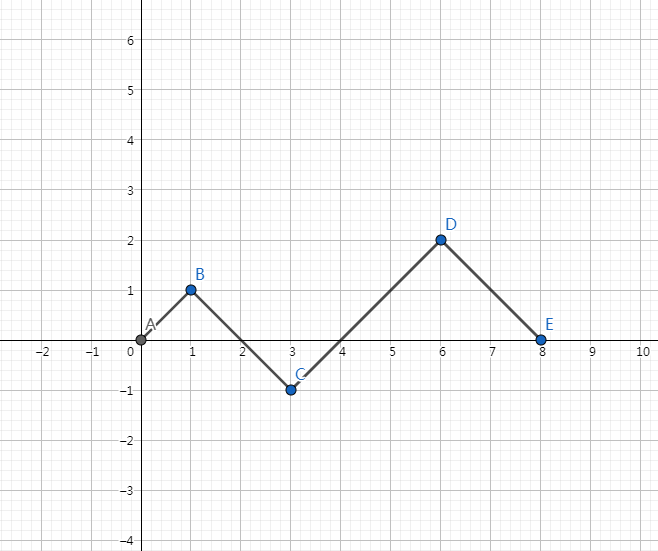
可知第一步一定向上，所以原题转化为从原点出发，轨迹在过程中不能跑到x轴下面。

枚举向上步数m，总方案数为C(n-1,m)，现在我们要减去非法方案数。对于非法的轨迹，有两种翻转方式：

把它第一次碰到y=-1前的轨迹按y=-1翻转（见P1641 [SCOI2010]生成字符串），也就是从（0，-2）到达原先的终点的方案与不合法方案一一对应，会发现向上走的步数比翻转前多1，即得C（n，m+1）
把它第一次碰到y=-1后的轨迹按y=-1翻转（如图2），在n，m确定的情况下，终点是确定的，翻转后的轨迹和原轨迹的方案一一对应。那么终点在哪里呢？设p为翻转后终点纵坐标，m为翻转前的向上步数，则有m - (n - m) + p = -2 （n-m为向下走的步数，翻转前终点纵坐标+1=翻转后纵坐标的相反数-1）-> p = -2 + n - 2m ，设当向上走x步时可以到达p，则 x - (n - x) = -2 + n - 2m -> x = n - m - 1，由于翻转后的轨迹和原轨迹的方案一一对应，所以到达p的方案数就是不合法的方案数

所以非法方案数为C(n,n-m-1)=C(n,m+1)，（见组合数中的互补性质，即从m个不同元素中取出n个元素的组合数=从m个不同元素中取出(m-n)个元素的组合数）

枚举向上步数为m，总方案数为C(n,m)-C(n,m+1);

公式（n已减1，n-1步没有不合法方案特判，n/2≤m（第一个人杀的次数）≤n-1）：

$C_{n-1}^{n-1}+\sum\limits_{i=\left\lfloor\frac{n}{2}\right\rfloor}^{n-2}(C_{n-1}^{i}-C_{n-1}^{i+1})=\sum\limits_{i=\left\lfloor\frac{n}{2}\right\rfloor}^{n-1}C_{n-1}^i-\sum\limits_{i=\left\lfloor\frac{n}{2}\right\rfloor+1}^{n-1}C_{n-1}^{i}=C_{n-1}^{\left\lfloor\frac{n}{2}\right\rfloor}$（公式来自@Alpha）

答案为C(n-1,n/2)

图2

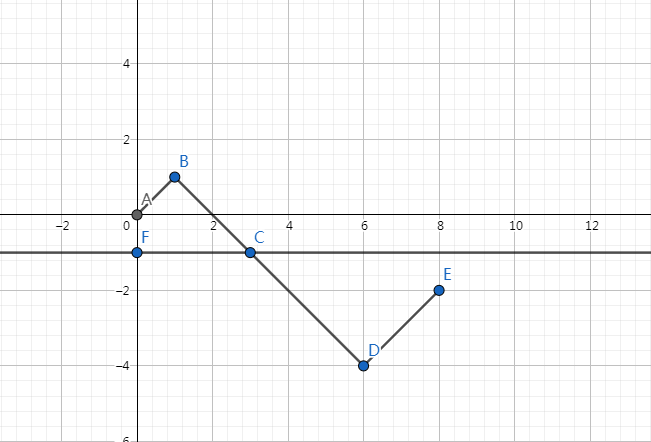
（以上思路由这个博客改进而来）

代码1

fac[i]存1~i的阶乘

inv[i]存1~i逆元的乘积

#include<cstdio>

using namespace std;

#define p 1000000007

long long fac[1000005],inv[1000005];

inline long long C(int n,int m) {

	if (n==m || m==0) return 1;

	return fac[n]*inv[m]%p*inv[n-m]%p;

}

int main() {

	int T,n;

	scanf("%d",&T),fac[0]=inv[0]=inv[1]=1;

	for (int i=1; i<1000005; i++) fac[i]=fac[i-1]*i%p;

	for (int i=2; i<1000005; i++) inv[i]=p-(p/i)*inv[p%i]%p;

	for (int i=2; i<1000005; i++) inv[i]=inv[i-1]*inv[i]%p;

	while(T--)

		scanf("%d",&n),printf("%lld\n",C(n-1,n/2));

}

代码2

#include<cstdio>

using namespace std;

#define p 1000000007

#define int long long

int fac[1000005];

inline int pow(int x) {

	int ans=1;

	x%=p;

	for (int i=p-2; i; i>>=1,x=x*x%p)

		if (i&1) ans=ans*x%p;

	return ans;

}//快速幂求逆元（x^(p-2)）

signed main() {

	int T,n;

	scanf("%lld",&T),fac[0]=1;

	for (int i=1; i<=1000005; i++) fac[i]=fac[i-1]*i%p;

	while(T--)

		scanf("%lld",&n),printf("%lld\n", fac[n-1]*pow(fac[n/2]*fac[n-1-n/2]%p)%p);

}

通过这题的确对组合数的应用加深了不少，如果分析有误还望指出qwq！

参考文章：

最后再次感谢@Alpha的耐心讲解与图例公式^_