密码 | 对称加密

一、AES 算法简介

高级加密标准（英语：Advanced Encryption Standard，缩写：AES），在密码学中又称Rijndael加密法，是美国联邦政府采用的一种区块加密标准，用来替换原先的 DES.
背景介绍：1997年1月2号，美国国家标准技术研究所（National Institute of Standards and Technology: NIST）宣布希望征集高级加密标准（Advanced Encryption Standard: AES），用以取代DES。AES得到了全世界很多密码工作者的响应，先后有很多人提交了自己设计的算法。最终有5个候选算法进入最后一轮：Rijndael，Serpent，Twofish，RC6和MARS。最终经过安全性分析、软硬件性能评估等严格的步骤，Rijndael算法获胜。

AES 算法的区块长度固定为128位（16 字节），密钥长度则可为128位，192位，256位。加密模式可采用 ECB，CBC，CTR，OFB，CFB 等模式进行加密。
其中 ECB 与 CBC 模式是对数据原文做加密处理，原文长度的必须为 16 或 16 的倍数方可加密成功，不足16倍数的部分则需进行 Padding 处理（Padding 方式为 PKCS5 Padding 或 PKCS7 Padding）。
CTR，OFB，CFB 模式则是对待加密数据的 IV 做加密处理，原文长度不需为 16 或 16 的倍数，原文长度与密文长度相等。
AES 属于对称加密即加密密钥与解密密钥是相同的，加密速度快。

二、AES 加密原理

AES 是分组密码技术，将明文进行分组加密，每组为固定128位（16字节）区块长度，不足 128 位的部分需采用补位方式，将其补全成为 128 位数据后进行加密。AES密钥区块长度可为 128位，192位，256位区块长度，加密过程中采用 Rijndael 提出的特定的密钥生成方案。
\[
\begin{array}{c|ccccc}{AES} & {密钥长度} & {加密轮数} \\ \hline 128 & {16字节} & {10轮} \\ {192} & {24字节} & {12轮}\\ {256} & {32字节} & {14轮} \end{array}
\]

加解密步骤：
AES 加密分为 4步。

SubBytes()，ShiftRows()，MixColumns()，AddRoundKey()。
AES 解密分为 4步。
逆向 MixColumn 子层, 逆向 ShiftRow 子层, 逆向 SubBytes 层，逆向 AddRoundKey()。

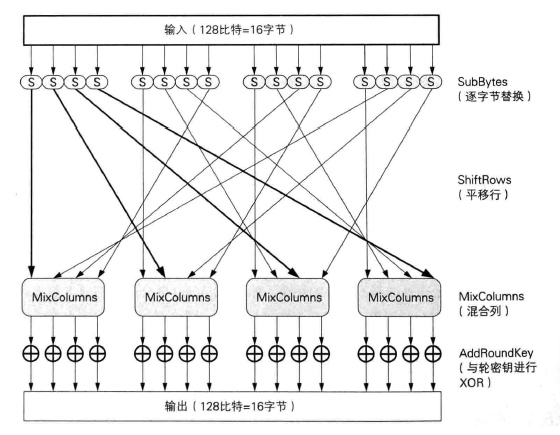
SubBytes()

字节替换，AES 定义了一个 16(0~F) * 16(0~F) 字节的 S 盒（S-Box)，将输入的数据 16 byte(4 * 4) 按照 S 盒的内容进行依次替换。例如数据为0x31，则需找到 S-Box 中横坐标为 3 纵坐标为 1 的值，进行替换操作。
\[
\begin{array}{c|ccccc}{\times} & {0} & {1} & {…} & {e} & {f} \\ \hline 0 & {x} & {x} & {x} & {x} & {x} \\ {1} & {x} & {x} & {x} & {x} & {x} \\ {…} & {x} & {x} & {x} & {x} & {x} \\ {e} & {x} & {x} & {x} & {x} & {x} \\ {f} & {x} & {x} & {x} & {x} & {x}\end{array}
\]

ShiftRows()

ShiftRows 行位移变换是状态数组的第一行保持不变，第二行循环左移一个字节，第三行循环左移两个字节，第四行循环左移三个字节。行移位变换的目的就是增加 AES 的扩展属性。
\[
\left(\begin{array}{llll}{B_{0}} & {B_{4}} & {B_{8}} & {B_{12}} \\ {B_{1}} & {B_{5}} & {B_{9}} & {B_{13}} \\ {B_{2}} & {B_{6}} & {B_{10}} & {B_{14}} \\ {B_{3}} & {B_{7}} & {B_{11}} & {B_{15}}\end{array}\right)
\]
经过 ShiftRows 操作结果为：
\[
\left(\begin{array}{llll}{B_{0}} & {B_{4}} & {B_{8}} & {B_{12}} \\ {B_{5}} & {B_{9}} & {B_{13}} & {B_{1}} \\ {B_{10}} & {B_{14}} & {B_{2}} & {B_{6}} \\ {B_{15}} & {B_{3}} & {B_{7}} & {B_{11}}\end{array}\right)
\]

MixColumns()

MixColumns 列混淆变换是一个线性变换，混淆了状态矩阵的每一列。列混淆变换中，每输入的一个字节均影响了 4 个输出字节，MixColumn 操作是 AES 中的主要扩散元素。ShiftRows() 和 MixColumns() 组合操作使得三轮以后，状态矩阵的每个字节都依赖于所有 16 个明文字节成为可能。
\[
\left(\begin{array}{l}{C_{0}} \\ {C_{1}} \\ {C_{2}} \\ {C_{3}}\end{array}\right)=\left(\begin{array}{llll}{02} & {03} & {01} & {01} \\ {01} & {02} & {03} & {01} \\ {01} & {01} & {02} & {03} \\ {03} & {01} & {01} & {02}\end{array}\right)\left(\begin{array}{l}{B_{0}} \\ {B_{5}} \\ {B_{10}} \\ {B_{15}}\end{array}\right)
\]
同理输出字节（C4，C5，C6，C7）的第二列是通过四个输入字节（B4，B9，B14，B3）与同一个常数矩阵相乘得到的，依此类推。计算法则按照伽罗瓦域内加减乘逆进行计算。

AddRoundKey()

密钥加法层是将 16 字节的当前状态矩阵和 16 字节的子密钥通过按位 XOR 操作结合在一起的。
\[
\left(\begin{array}{llll}{A_{0}} & {A_{4}} & {A_{8}} & {A_{12}} \\ {A_{1}} & {A_{5}} & {A_{9}} & {A_{13}} \\ {A_{2}} & {A_{6}} & {A_{10}} & {A_{14}} \\ {A_{3}} & {A_{7}} & {A_{11}} & {A_{15}}\end{array}\right)\left(\begin{array}{llll}{K_{0}} & {K_{4}} & {K_{8}} & {K_{12}} \\ {K_{1}} & {K_{5}} & {K_{9}} & {K_{13}} \\ {K_{2}} & {K_{6}} & {K_{10}} & {K_{14}} \\ {K_{3}} & {K_{7}} & {K_{11}} & {K_{15}}\end{array}\right) = \left(\begin{array}{llll}{A_{0} \wedge K_{0}} & {A_{4} \wedge K_{4}} & {A_{8} \wedge K_{8}} & {A_{12} \wedge K_{12}} \\ {A_{1} \wedge K_{1}} & {A_{5} \wedge K_{5}} & {A_{9} \wedge K_{9}} & {A_{13} \wedge K_{13}} \\ {A_{2} \wedge K_{2}} & {A_{6} \wedge K_{6}} & {A_{10} \wedge K_{10}} & {A_{14} \wedge K_{14}} \\ {A_{3} \wedge K_{3}} & {A_{7} \wedge K_{7}} & {A_{11} \wedge K_{11}} & {A_{15} \wedge K_{15}}\end{array}\right)
\]

三、AES 模式说明

分组密码算法（DES，AES，SM4等）只能加密固定长度的分组，当待加密明文数据长度都超过分组密码长度时，就需要对分组密码算法进行迭代，将明文数据进行加密，迭代的方法称为分组密码的模式。

ECB 模式

ECB 模式全称为电子密码本模式，ECB 模式中，将明文分组加密之后的结果直接拼接成密文分组。
ECB 模式中相同的明文分组会被转换成为相同的密文分组。
计算支持并行计算（加密，解密）。

ECB 模式存在非常大的风险，攻击者不需要破译密码就可以操作明文。

分组1：卡号A

分组2：金额1

分组3：卡号B

交易信息为卡号A 向卡号B 转账 金额1，攻击者将分组信息对调成 卡号B 向卡号A 转账 金额1，攻击者无需解析密文，就能更改交易信息，显然是存在风险的。

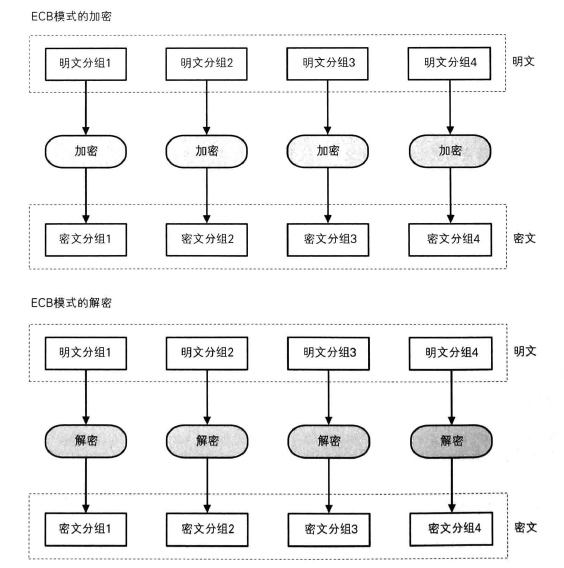
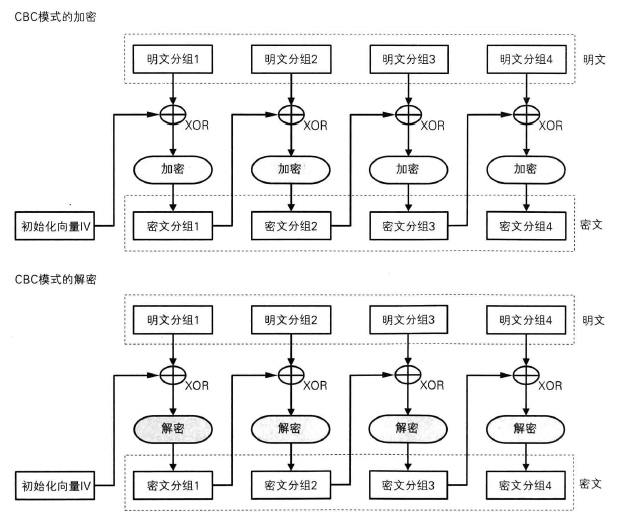
CBC 模式

CBC 模式全称为密码分组链接模式，CBC 模式中加密过程引入初始化向量 IV，第一包数据与初始化向量 IV 做异或操作后进行加密，接下来将明文分组与前一个密文分组进行异或操作后在进行加密。
计算支持并行计算（仅解密）。

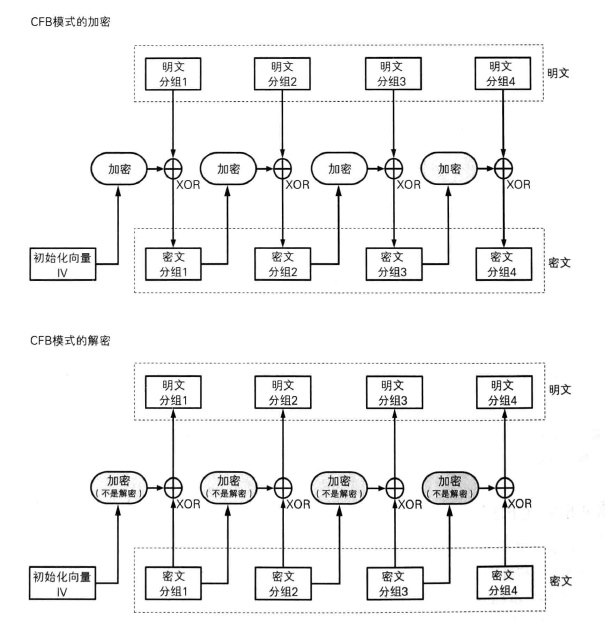
CFB 模式

CFB 模式为密文反馈模式，在 CFB 模式中，明文分组并没有直接进行加密，第一包数据将初始化向量加密，密文值与明文分组进行异或操作，接下来依次将每次异或得到的结果进行加密得到数据密文。
计算支持并行计算（仅解密），可以解密任意分组。

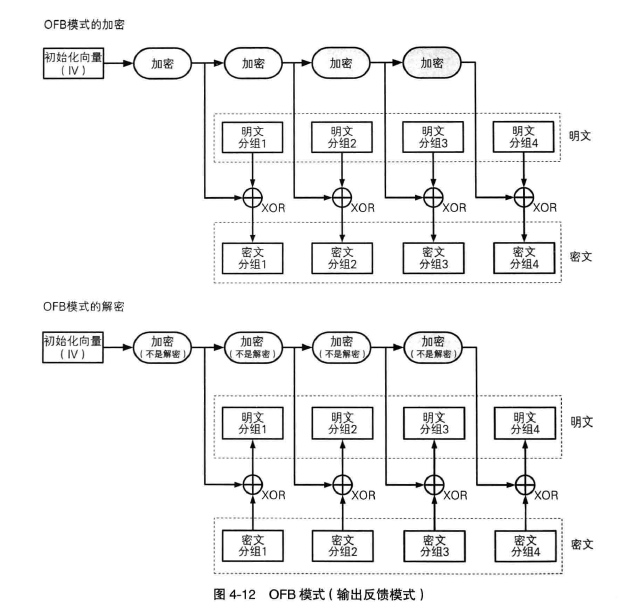
OFB 模式

OFB 模式为输出反馈模式，OFB 模式中，密码算法的输出会反馈到密码算法的输入中。OFB 模式中，XOR 所需要的比特序列可以事先通过密码算法生成，和明文分组无关。只要提前准备好所需的密钥流，则在实际从明文生成密文的过程中，就不需要动态密码算法了。
计算不支持并行计算（加密，解密）。

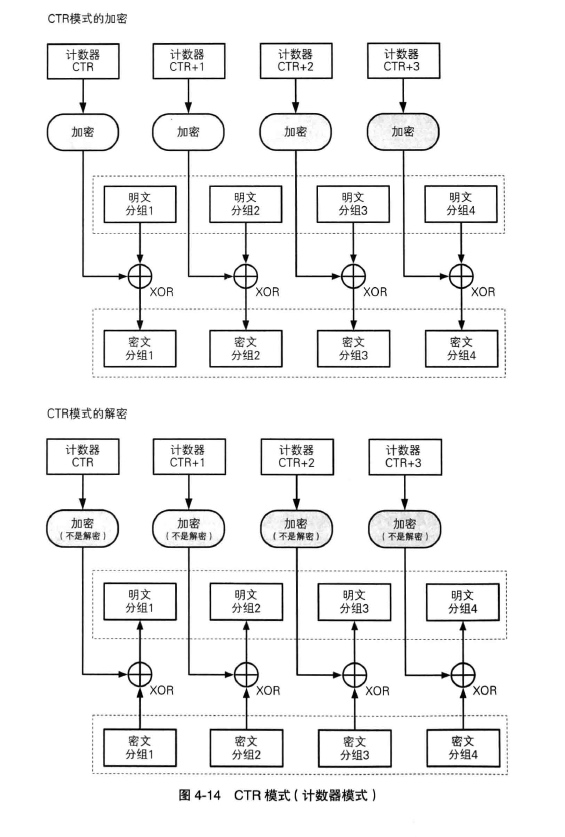
CTR 模式

CTR 模式为计数器模式，CTR 模式是一种通过将逐次累加的计数器进行加密来生成密钥流的流密码。CTR 模式中，每个分组对应一个逐次累加的计数器，并通过对计数器进行加密来生成密钥流。最终的密文分组是通过将计数器加密得到的比特序列，与明文分组进行异或得到。CTR 模式可以以任意顺序对分组进行加解密，在加解密时需要用到的 “计数器” 的值可以由分组序号直接计算出来，可以实现并行计算，支持并行计算的系统中，CTR 模式的速度非常快。CFB，OFB 模式均推荐使用 CTR 模式代替。
支持并行计算（加密，解密）。

四、参考

参考链接：
https://en.wikipedia.org/wiki/Advanced_Encryption_Standard
http://csrc.nist.gov/encryption/aes/rijndael/Rijndael.pdf
http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf
https://bbs.pediy.com/thread-253884.htm

参考书籍：
《深入浅出密码学》
《图解密码技术》

参考代码：
LGPL-AES:https://tls.mbed.org/source-code